মধ্যযুগের জ্ঞান-বিজ্ঞান সম্বন্ধে আলােচনা করতে গেলে অনিবার্যভাবে আরব তথা মুসলমানদের কথা এসে পড়ে। আমাদের মনে হয়েছে মধ্যযুগীয় বলে এই যুগটিকে ইচ্ছাকৃত উপেক্ষা করা হয়। কেউ কেউ বলেছেন তাদের সবটাই অনুবাদ, মৌলিক কোন কাজ নেই, কেউ বলেছেন অপরিণত কাজ-কর্ম, আবার কেউ কেউ তাদের কৃতিত্ব বেমালুম চেপে গিয়ে পরবর্তী ইউরােপীয় বিজ্ঞানীদের সমস্ত কৃতিত্ব দিয়েছেন। অথচ চিকিৎসা, গণিত (অ্যালজাবরা, জ্যামিতি, ত্রিকোণমিতি), মহাকাশবিদ্যা, ভূগােল, রসায়ন, জীববিদ্যা, উদ্ভিদবিদ্যা, ভৌতবিজ্ঞান, প্রযুক্তি প্রভৃতি বিজ্ঞানের বিভিন্ন শাখাগুলি এই সময়ই আকার পেতে থাকে। আর-রাযী, আল খােয়ারিজমী, আল বাত্তানি, আল ফারগানী, আল ইদরীসী, জাবির, আল আসমায়ী, আন-নাফিস প্রমুখ বিজ্ঞানী ও প্রযুক্তিবিদ বিজ্ঞানের বেশ কয়েকটি শাখার জনক। অনেকেই বিশ্বাস করেন সূর্যকেন্দ্রিক সৌরজগতের ধারণা প্রথম দিয়েছিলেন আলবিরুনী, পরে নাসিরউদ্দিন তুসি, আধুনিক বীজগণিতের জনক আল খােয়ারিজমী, আল ইদরীসী প্রণীত মানচিত্রে ৭টি মহাদেশের চিত্রই আছে ইত্যাদি।
তাছাড়া সৌরকলঙ্কের আবিষ্কার, সৌরকক্ষের উৎকেন্দ্রিকতা, সূর্যের মন্দোচ্চতা, ভ্রান্তি বৃত্তের বক্রতার ক্রমিক হ্রাস, ক্রান্ত গমনের পরিমাণ ইত্যাদি সূক্ষ্ম গণনার দ্বারা তারা গণিত শাস্ত্রের অভূতপূর্ব উন্নতি সাধন করে গেছেন। বর্তমান ত্রিকোণমিতির উদ্ভাবন, কিউবিক ইকুয়েশানের সমাধান, ব্যাস ও সমাহার গণিতের সৃষ্টিও আরবগণ দ্বারাই আবিষ্কৃত। John William Draper 05 History of the Intellectual Development of Europe’ alce opgelos 16610, “Not one of the purely Mathematical, mixed or practical sciences was ommitted by the Arabs.” মুসলমানগণ বীজগণিত আবিষ্কার করেন এবং একে পূর্ণাঙ্গরূপ দান করেন। তারাই সর্বপ্রথম ইউক্লিডের এলিমেন্টস ও জ্যামিতি অনুবাদ করেন। প্রফেসার আরনল্ডের মতে,
“প্রকৃতপথে মুসলমানগণই সমতল ক্ষেত্র, গােলাকার ত্রিকোণমিতির প্রতিষ্ঠাতা। এটি প্রকৃতপথে গ্রীক পণ্ডিতদের জানা ছিল না।”
আরবগণই প্রথম দশমিক পদ্ধতি সৃষ্টি করেছেন। এম এ কাদের বলেন,
“শূন্যের ন্যায় দশমিক মানও মােহাম্মদ বিন মুসা আল খােয়ারিজমীর আবিষ্কার।”
ড্রেপার আরও একধাপ এগিয়ে বলেন, “বর্গীয় সমীকরণের সাধারণ নিয়মও আরবগণ আবিষ্কার করেন। তাঁরা পাশ্চাত্য জগতকে সংখ্যা গণনা পদ্ধতিও শিক্ষা দান করেছেন। এ জন্য আরবী প্রতীক এখনও পৃথিবীর সকল জাতি ব্যবহার করে। গণিতের Technical শব্দ algorism, surd, sine প্রভৃতি শব্দ আরবী ভাষা থেকে উৎপত্তি হয়েছে।” বীজগণিত ও আরবদের অন্যান্য আবিষ্কারগুলাে আরব নাবিক, বণিক ও সমুদ্রচারী লােকেরা ইউরােপ ও অন্যান্য দেশে বহন করে নিয়ে যেত। আরবগণ দ্বিতীয় পর্যায়ের সমীকরণ আবিষ্কার করে দ্বিঘাত সমীকরণ ও দ্বিপদ উপপাদ্যের উন্নতি সাধন করেন। তারা গ্রীক গণিত শাস্ত্রবিদদের গ্রন্থ সংগ্রহ ও অনুবাদ করেই ক্ষান্ত হননি, তারা নিজস্ব অবদানে একে সমৃদ্ধও করেন। প্রফেসর পি কে হিট্টি বলেন,
“The science of trigonometry, like algebra and analytical geometry, was largely founded by arabs.”
মুসলিম ইতিহাসের স্বর্ণযুগের এই অধ্যায়টি সম্পর্কে আমাদের পুনঃপাঠের প্রয়ােজনীয়তা দেখা দিয়েছে। আজ সবক্ষেত্রে পিছিয়ে পড়া মুসলমানদের ঐ অধ্যায়টিই হয়তাে প্রেরণার উৎস হতে পারে। কারণ পূর্বপূরুষদের থেকে শিক্ষা গ্রহণের সুযােগ মুসলমানদের সবচেয়ে বেশি। ইতিহাসে শিক্ষা এবং নৈতিকতার যে আদর্শ মুসলমানরা রেখে গেছেন, তা থেকে আমরা লাভবান হব। ভারত সরকার বুদ্ধিবৃত্তির উন্নতি এবং নৈতিকতা বিষয়ক পাঠ্যসূচীতে মুসলমানদের মধ্যযুগীয় ইতিহাস অন্তর্ভুক্ত করতে পারেন। অমুসলিমরা তাদের ধর্মের প্রতি আনুগত্যশীল থেকেও এগুলাে পাঠ করতে পারবেন এবং সঠিক সিদ্ধান্তে পৌঁছতে তাদের বেগ পেতে হবে না। আধুনিক ইউরােপ এবং আমেরিকা যে সভ্যতার বড়াই করছে, মুসলিম সভ্যতার কাছে তা ফিকে হয়ে যায়।
ঐতিহাসিকগণ অনবহিত নন যে, ইসলামের আবির্ভাবের পরপরই আরব দেশে গৌরবময় সভ্যতার সূত্রপাত হয়। সমরেন্দ্রনাথ সেন ‘বিজ্ঞানের ইতিহাস’ গ্রন্থে (আরব্য বিজ্ঞান অধ্যায়, পৃ. ১০৯) বলেছেন,
“আরব জাতির রাজনৈতিক অভ্যুত্থানের মত জ্ঞান-বিজ্ঞানে, শিক্ষায় ও সংস্কৃতিতে এবং সাধারণভাবে মানব-সভ্যতার উন্নয়নে এই জাতির বিরাট অবদান রীতিমত বিস্ময়কর। একেরবাদের মন্ত্রশক্তিবলে প্রবুদ্ধ শুষ্ক মরুভূমির ছন্নছাড়া ক্ষুধার্থ বেদুইন আরবদের ঐক্যবদ্ধ পরাক্রমশালী জাতিরূপে পৃথিবীর রাজনৈতিক রঙ্গমঞ্চে সহসা আবির্ভাব ও প্রধান ভূমিকা গ্রহণের ইতিহাস বাস্তবিকই চকমপ্রদ। তেমনই বিস্ময়কর তাহাদের অত্যল্পকালের মধ্যে মরুভূমির আদিম বর্বর জীবন পরিত্যাগ করিয়া জ্ঞান-বিজ্ঞানে, শিল্পে, সাহিত্যে, সমাজ ও রাজনৈতিক ব্যবস্থায় সভ্যতার উত্তুঙ্গ শিখরে আরােহণের বিচিত্র ইতিহাস। মানব-সভ্যতার ইতিহাসে ইসলামের অভ্যুদয় এক বৈপ্লবিক ঘটনা, এক বিরাট বিস্ফোরণ বিশেষ।”
এটা কিসের বলে সম্ভব হল? মুসলমানগণ তাদের সমস্ত শক্তি কুরআনের শিক্ষায় নিয়ােগ করে এ অসাধ্য সাধন করেছিলেন। এই পবিত্র গ্রন্থ তাদের মরুভূমির দূস্তরতাকে পরােয়া করার পরিবর্তে বীরের মতাে সামনে চলার অনুপ্রেরণা দিয়েছিল, এর প্রতিটি বাক্য যেন নবীন মুসলমানদের সামনে এক একটি সাহসের তরবারী হয়ে সকল বাধা-বিপত্তি জয় করতে এগিয়ে এসেছিল।
সমস্ত বিশ্বের ইতিহাস একদিকে রেখে যদি আধুনিক সভ্যতার কথা আলােচনা করি, তবে নিদ্বিধায় একথা সবাই স্বীকার করতে বাধ্য হবেন যে, কুরআনের আলােকই আধুনিক সভ্যতার উৎস-শক্তি। পন্ডিত আর ম্যারগােলিউথ বলেন, কুরআনের স্বাতন্ত্র নতুন সাহিত্য এবং দর্শনের বীজ বপন করেছিল। ইহূদী এবং খ্রিস্টানদের মেধা অন্বেষী মনকে কর্ষণ করে মধ্যযুগে প্রবলভাবে তাদের প্রভাবিত করেছিল পবিত্র কুরআন। মুসলিম বিধের অগ্রগতি ছিল বাধাপ্রাপ্ত কিন্তু গবেষণায় দেখা যায় যে, ইউরােপীয়রা যখন বর্বরতার পর্যায়ে, তখন মুসলমানদের দর্শন, অংকবিদ্যা এবং জ্যোতির্বিদ্যা ইউরােপীয়দের নতুন আলাে দেখায় যা তারা কয়েক শতাব্দী চেষ্টা করেও নাগাল পায়নি। ল্যাটিন মূলত আরবীর কাছেই ঋণী এবং কুরআনের শিক্ষা পরােক্ষ ভাবে আরববাসী এবং তাদের প্রতিবেশীগণ গ্রহণ করে পবিত্র কুরআনের শব্দ-ব্যঞ্জনা, কবিতা অথবা সাহিত্যের যে কোন ক্ষেত্রে কুরআনের পরােক্ষ প্রভাব ও প্রতাপ তাদেরকে সত্যিকার জ্ঞানী এবং শিক্ষিত করে তুলেছিল। বিখ্যাত প্রাচ্য বিশারদ ইমানুয়েল ডােটস্ এর মতে,
“একটি গ্রন্থ দিয়ে আরবরা সমস্ত বিশ্ব জয় করেছিলেন, যা ছিল মহান আলেকজান্ডারের বিজয়ের চেয়েও মহান রােম বিজয়ের চেয়েও বিস্ময়কর।”
অথচ এ যুগের কিছু মন-মানসিকতায় এ-কথা আবর্তিত হতে থাকে যে, বিজ্ঞান এমন একটা বিষয় যার সঙ্গে ইসলাম ও কুরআনের কোনও সম্পর্ক নেই। ইসলাম বিজ্ঞানের বিরােধিতা করে। বিজ্ঞানের গবেষণা ও আবিষ্কার ইসলামী দর্শন ও চিন্তাধারার সঙ্গে সামঞ্জস্যশীল নয়। ইসলামের বিরুদ্ধে অভিযােগকারীরা ইসলামের বিরুদ্ধে এই ধরনের ধারণা প্রচার করতে থাকে অহরহ। বিষােদগার পূর্ণ কথাবার্তায় সর্বদা আহত করতে থাকে ইসলামের অনুসারীদের। সাথে সাথে ইসলাম-বিরােধীদের এই ধরনের প্রােপাগাণ্ডা ও প্রচারে মুসলমানরা হীনম্মন্যতায় ভুগতে থাকে এবং নিজেদেরকে অনগ্রসর ও পশ্চাৎপদ সম্প্রদায় হিসাবে মনে করতে থাকে। কিন্তু প্রকৃত বাস্তব এর সম্পূর্ণ বিপরীত।
তাহলে যে কুরআনের বিরুদ্ধে তাদের এত অভিযােগ সেই কুরআন এবার খতিয়ে দেখা যাক। বস্তুত গােটা কুরআনে এমন একটি বাক্যও নেই যা বিজ্ঞানী-বিরােধী। বরং কুরআনে এমন অসংখ্য বাক্য রয়েছে যেসবে এই বিধব্যবস্থাকে উপলব্ধি করার, তা নিয়ে গভীর চিন্তাভাবনা করার এবং প্রাকৃতিক ঘটনাবলী ও দৃশ্যাবলী পর্যবেক্ষণ করার আমন্ত্রণ জানানাে হয়েছে। কুরআনই প্রথম গ্রন্থ যাতে দৃশ্যমান প্রকৃতি সম্বন্ধেগভীর গবেষণা করার ও তা থেকে উপকৃত হওয়ার এবং এর উদ্দেশ্য ও লক্ষকে উপলব্ধি করে এ থেকে ফায়দা অর্জন করার হুকুম দেওয়া হয়েছে।
নানা উত্থান-পতনের মধ্য দিয়ে মানবজাতি যখন ইতিহাসের পথ পরিক্রম করছিল, জ্ঞান-বিজ্ঞান যখন অবহেলিত ছিল, বিদ্যাচর্চা যখন অন্যায় বা পাপ বলে বিবেচিত হত,পৃথিবীকে গােলাকার বলা যখন অপরাধ ছিল, জ্ঞানচর্চার অপরাধে হিপাসিয়াএর দেহকে আলেকজান্দ্রিয়ার গীর্জায় খন্ড-বিখন্ড করা হয়েছিল, গ্যালিলিওকে আত্মহুতি দিতে হয়েছিল রােমের পবিত্র গীর্জায়, বিবর্তনবাদে বিধাসের জন্য বিজ্ঞানী ভেনিনি-এর জিহ্বা ছিঁড়ে ফেলা হয়েছিল ও আগুনে জীবন্ত পুড়ে হত্যা করা হয়েছিল, যখন মহান গ্রেগরি রােম হতে সকল শিক্ষিত লােককে বহিষ্কৃত করেছিলেন, অগাষ্টাসের বিখ্যাত দর্শনশাস্ত্রের পাঠাগারে আগুন লাগিয়ে দেওয়া হয়েছিল এবং গ্রীক ও রােমান গ্রন্থপাঠ কঠোরভাবে নিষিদ্ধ হয়েছিল, সেই অন্ধকার ও কুসংস্কারাচ্ছন্ন যুগসন্ধিক্ষণে ইসলাম শান্তি, শিক্ষা, জ্ঞান-বিজ্ঞান ও সভ্যতার আলােকবর্তিকা নিয়ে পৃথিবীর বুকে আবির্ভূত হয় এবং সকল কুসংস্কার ভেঙে চুরমার করে প্রতিষ্ঠিত করে জ্ঞানের মহাসমুদ্র। আবহমানকাল ধরে মানুষের একটা ধারণা ছিল যে, বিজ্ঞান ধর্ম থেকে পৃথক বিষয়। কিন্তু ইসলাম সে ধারণাকে পদাঘাত করে বিজ্ঞানকে ধর্মের রন্ধ্রে রন্ধ্রে অনুপ্রবেশের স্থান দিয়েছে। তাই ফরাসী বিজ্ঞানী মরিস বুকাইলী অকুণ্ঠচিত্তে বলেন,
“ইসলামে ধর্ম ও বিজ্ঞানকে যমজ বােন হিসেবে গণ্য করা হয়।
তিনি আরও বলেন, “
কুরআনে অগ্রহণযােগ্য কোন বৈজ্ঞানিক বিবৃতি পাওয়া যায় না।”
কুরআনের বাক্যসমূহ লক্ষ্য করলে দেখা যায় আকাশ, চাদ, সূর্য, নক্ষত্র, গ্রহ, পাহাড়, সমুদ্র, নদনদী, জীবজন্তু এমনকী আকাশ ও পৃথিবীতে বিদ্যমান প্রতিটি বস্তু ও বিষয়ের প্রতি ভাবনাচিন্তা ও গবেষণা করার তাগাদা দেওয়া হয়েছে। বার বার কুরআনে সুস্পষ্টভাবে বলা হয়েছে “তবে কি তারা উটের প্রতি লক্ষ করে না, কিভাবে তা সৃষ্টি করা হয়েছে? আর লক্ষ্য করে কি আসমানের দিকে, কিভাবে তা ঊর্ধ্বে স্থাপন করা হয়েছে? এবং পর্বতমালার দিকে, কিভাবে তা শক্ত করে দাঁড় করানাে হয়েছে এবং স্থলভাগের দিকে, কিভাবে তা সমতলে বিছানাে হয়েছে?” (সূরা গাশিয়া ১৭-২০) “আকাশ ও পৃথিবীর সৃষ্টিতে, রাত্রি ও দিনের পরিবর্তনে, মানুষের উপকারে যা লাগে তা দিয়ে জাহাজের সমুদ্রযাত্রায়, সেই বৃষ্টি যা আল্লাহ্ আকাশ থেকে বর্ষণ করেন, যার দ্বারা মৃত পৃথিবীকে পুনরুজ্জীবিত করেন ও সেখানে যাবতীয় জীবজন্তুর বিস্তার ঘটান, সেই বায়ুপ্রবাহের পরিবর্তনে এবং আকাশ ও পৃথিবীর সেবায় নিয়ােজিত সেই মেঘমালায়—জ্ঞানী লােকদের জন্য তাে বহু নিদর্শন রয়েছে।” (সূরা বাকরা ১৬৪)।
“তার নিদর্শনাবলীর মধ্যে একটি নিদর্শন এই যে, তিনি তােমাদের মাটি থেকে সৃষ্টি করেছেন। এখন তােমরা সর্বত্র ছড়িয়ে পড়েছ। আর তার নিদর্শনাবলীর মধ্যে আর একটি নিদর্শন—তিনি তােমাদের জন্য তােমাদের মধ্য থেকে তােমাদের সঙ্গিনীদের সৃষ্টি করেছেন, যাতে তােমরা ওদের কাছে শান্তি পাও, আর তােমাদের মধ্যে পরস্পরের প্রতি প্রেম ও স্নেহ সৃষ্টি করেছেন। চিন্তাশীল সম্প্রদায়ের জন্য এতে অবশ্যই নিদর্শন রয়েছে। আর তাঁর নিদর্শনাবলীর মধ্যে অন্যতম নিদর্শন, আকাশ ও পৃথিবীর সৃষ্টি এবং তােমাদের ভাষা ও বর্ণের বৈচিত্র। এতে জ্ঞানীদের জন্য অবশ্যই নিদর্শন রয়েছে।” (সূরা রূম ২০-২২) “দিন ও রাত্রির পরিবর্তনে এবং আল্লাহ আকাশ ও পৃথিবীতে যা সৃষ্টি করেছেন তাতে সাবধানী সম্প্রদায়ের জন্য নিদর্শন রয়েছে।” (সূরা ইউসূফ ৬) “তিনি তােমাদের বিশ্রামের জন্য রাত্রি ও দেখার জন্য দিন সৃষ্টি করেছেন। যে সম্প্রদায় কথা শােনে তাদের জন্য নিশ্চয়ই এতে নিদর্শন রয়েছে।” (সূরা ইউসুফ ৬৭) “তারা কি লক্ষ্য করে না পাখি আকাশের শূন্যে সহজেই ঘুরে বেড়ায়? আল্লাহই ওদের স্থির রাখেন। এর মধ্যে তাে নিদর্শন রয়েছে বিশ্বাসী সম্প্রদায়ের জন্য।” (সূরা নাহল ৭৯) “তােমরা কি লক্ষ্য করনি আল্লাহ্ কিভাবে সৃষ্টি করেছেন সাত স্তরে সাজানাে আকাশ আর সেখানে চন্দ্রকে আলাে হিসাবে এবং সূর্যকে প্রদীপ হিসাবে স্থাপন। করেছেন।” (সূরা নূহ ১৫-১৬)।
কুরআন থেকে মাত্র কয়েকটি দৃষ্টান্ত উপস্থাপন করা হল এখানে। কিন্তু কুরআনে রয়েছে আরও এরকম অসংখ্য দৃষ্টান্ত। এসব বাক্যে এ-কথা স্পষ্ট করা হয়েছে যে, এই বিজগতে রয়েছে আল্লাহর অগণিত নিদর্শন। এসব নিদর্শন জ্ঞানী ব্যক্তিদের সােজা-সরল পথ প্রদর্শন করে। এসব নিদর্শন নিয়ে ভাবনা-চিন্তা করার কথা বিশেষভাবে বলা হয়েছে কুরআনে।
নােবেল জয়ী বিজ্ঞানী আব্দুস সালাম বলছেন, কুরআনে প্রাকৃতিক নিয়মাবলীর উপর জোর দেওয়া হয়েছে। কাজেই আমার বিজ্ঞান সংক্রান্ত ধারণায় ইসলামের এক মস্ত অবদান রয়েছে। আব্দুস সালাম জোর দিয়ে বলেন, ‘৭৫০ থেকে ১২০০ সাল পর্যন্ত বিজ্ঞানচর্চার প্রায় পুরােটাই হয়েছিল ইসলামী ছত্রছায়ায়, আমি সেই পতাকারই বাহক মাত্র। উল্লেখ্য, ১৯৯০ সালে আলিগড় মুসলিম বিশ্ববিদ্যালয়ে আব্দুস সালাম ভাষণ দিয়েছিলেন। ভাষণ শেষে কেউ তাকে প্রশ্ন করেছিলেন, এখন তিনি কি নিয়ে কাজ করছেন? উত্তরে তিনি দুটি বিষয় উল্লেখ করেছিলেন। এক হচ্ছে—বিজ্ঞান ও প্রযুক্তিবিদ্যার বিকাশকে কাজে লাগিয়ে তৃতীয় দুনিয়ার দেশগুলিকে আর্থিক ও সামাজিক ক্ষেত্রে উন্নত করার পরিকল্পনা রচনা, এবং দুই হচ্ছে কুরআনে বিজ্ঞান ও প্রযুক্তির ইঙ্গিত বহনকারী যে সব বাক্যগুলি আছে ব্যাখ্যাসহ তার সংকলন বের করা। আব্দুস সালামের সেই ধরনের কোন সংকলন বের হয়েছে কিনা জানা নেই। তবে ইসলামিক ফাউন্ডেশন বাংলাদেশ প্রকাশিত গ্রন্থ ‘সায়েন্টিফিক ইন্ডিকেশনস ইন দ্য হলি কুরআন’ আমরা সংগ্রহ করতে পারি।
এসব অধ্যয়ন করার পর কি বলা যেতে পারে যে ইসলাম বিজ্ঞান-বিরােধী। বরং ইসলাম ধর্মাবলম্বী মুসলিমরাই বিজ্ঞানের শাখাগুলিকে নানাভাবে পুষ্ট করেছে। তবে আমরা এখানে কেবল গণিত শাস্ত্র নিয়ে একটা সংক্ষিপ্ত আলােচনা করব। বিজ্ঞানে গণিত শাস্ত্রের অবস্থান ‘মা’-র মতাে। সকল বিজ্ঞানের সূত্রপাত গণিত শাস্ত্র হতেই। কোথা হতে এ শাস্ত্র আলােচনা আরম্ভ হয়েছিল নিশ্চিত জানা না গেলেও মানুষের প্রয়ােজনে হিসাবের ব্যবহার যে আদিযুগেই শুরু হয়েছিল এ সম্পর্কে কোনও অনুসন্ধানের অপেক্ষা করতে হয় না। অনেকে মেসােপটেমিয়া ও মিশরকে গণিত শাস্ত্রের আদি ভূমিরূপে চিহ্নিত করেন। এ দৌড়ে চীন ও ভারতবর্ষও কম যায় না। সে যাই হােক, মানুষের জীবনের সাথে ওতপ্রােতভাবে জড়িত এই শাস্ত্র যে বহু সভ্যতায় অনুচর্চিত হয়েছিল এবং নানা পর্বে উন্নতি লাভ করেছিল তা নিশ্চিত।
মুসলিম যুগে গণিত শাস্ত্রের প্রাথমিক অনুপ্রেরণা আসে কুরআন হতে। কুরআনে সংখ্যা বিজ্ঞান এবং হিসাব বিজ্ঞানের যে ধারণা দেওয়া হয়েছে তা মূলত এসেছে এক আল্লাহর একত্ববাদ হতে। সাঈদ হােসেন তার ইসলামিক সায়েন্স গ্রন্থে গাণিতিক মতবাদ প্রসঙ্গে লিখেছেন,
“মানুষের অন্তরে সংখ্যার অবয়বগুলি জড়বস্তুতে অস্তিত্ববান অবয়বের অনুরূপ। ইহা ঊর্ধ্বলােকের একটি নমুনা। গণিতের জ্ঞানের মাধ্যমে একজন তপস্বী ক্রমান্বয়ে অন্যান্য গাণিতিক ও প্রাকৃতিক বিজ্ঞান এবং অধিবিদ্যা সম্পর্কিত জ্ঞানের উচ্চস্তরে উন্নীত হয়। সংখ্যাবিজ্ঞান বিজ্ঞানসমূহের বুনিয়াদ, জ্ঞানের মৌল উপাদান, বিজ্ঞানের মূল।”
কুরআনে সংখ্যাচর্চা বিষয়ক অনেক বাক্য রয়েছে। সুরা মু’মিন-এ বলা হয়েছে, “আল্লাহ বলবেন, তােমরা পৃথিবীতে কত বছর অবস্থান করছিলে? ওরা বলবে, আমরা অবস্থান করেছিলাম একদিন বা একদিনের কিছু অংশ।” আল্লাহর অফুরন্ত করুণা সম্পর্কে বলা হয়েছে, “যদি তােমরা আল্লাহর অনুগ্রহসমূহ গণনা কর, তবে এর সংখ্যা নির্ণয় করতে তােমরা পারবে না।” এছাড়া মুসলিম নারীর তালাক ও ইদ্দত, কাফিরদের শাস্তি, ক্রয়-বিক্রয়, সূর্য ও চন্দ্রের পরিক্রমণ, সৃষ্টি প্রত্রিয়া, উত্তরাধিকার আইন, রমজান, যাকাত ফিতরা, বিচার ও অন্যান্য অনেক উপলক্ষে গণনা ও হিসাবের আওতাভুক্ত। এ সকল বিষয় মুসলিম বিজ্ঞানীদের গণিত চর্চায় উদ্বুদ্ধ করেছে বললে অত্যুক্তি হয় না। আফযালুর রহমান লিখেছেন,
“ইসলামের ইতিহাসের প্রাথমিক পর্যায়ে সংখ্যাসমূহের প্রতীকী ভূমিকা গণিত চর্চায় গুরুত্বপূর্ণ অবদান রাখিয়াছে।…কুরআন চর্চার প্রেরণাই গণিতের ক্ষেত্রগুলিতে বিরাট গবেষণার সহায়ক হইয়াছে এবং মুসলিম বিজ্ঞানীরা গণিতের ক্ষেত্রে নয়া নানাবিধ প্রয়ােগ-পদ্ধতি উদ্ভাবনে সক্ষম হইয়াছেন।”
হযরত মােহাম্মদের (সাঃ) প্রয়ানের পর অনেকের মতে, তার জীবিতকালেই হিজরী সন গণনা আরম্ভ হয়ে যায়। অন্য মতে, দ্বিতীয় খলিফা হযরত উমার ৬৩৮/৩৯সালের দিকে হিজরী সন চালু করেন শাসনব্যবস্থা সূদৃঢ় করতে। ৬২২ সালের ২০ সেপ্টেম্বর হিজরতের প্রকৃত তারিখ হলেও ৬২২ সালের ১৫ জুলাই শুক্রবার হতে হিজরী সনের যাত্রা আরম্ভ হয়। পঞ্জিকা তথা তারিখ নির্ধারণের ব্যবস্থা হওয়ার পর মুসলমানরা আরবী অক্ষরসমূহকে ‘আবজাদ’ সংখ্যামালার গণনা অনুযায়ী ব্যবহার করা শুরু করে। আরবী বর্ণের সাংখ্য মানগুলাে হল,
আলিফ -১, ত্বা – ৯, ফ, – ৮০, যা- ৭০০, বা – ২ ইয়া -১০, ছােদ্ব -৯০, দ্বোত্ -৮০০, জ্বিম – ৩, কাফ – ২০, কাফ – ১০০, জোয়া – ৯০০, দ্বাল – ৪, লাম – ৩০, রা – ২০০, গাইন – ১০০০, ছােট হা – ৫, মীম – ৪০, সীন – ৩০০, ওয়াত – ৬, নুন – ৫০, তা – ৪০০, যা – ৭, ছিন – ৬০, ছা – ৫০০, বড় হা – ৮, আইন – ৭০, খা – ৬০০,
বিজ্ঞান হিসাবে এর স্থান যেখানেই হােক না কোন সুসংবদ্ধ গণনা পদ্ধতির নিয়মের এটি ছিল প্রাথমিক প্রচেষ্টা। যষ্ঠ শতাব্দীর পর মুসলিম বিজয় বিব্যাপী ব্যাপ্ত হলে এবং সাম্রাজ্য প্রতিষ্ঠিত ও নির্বিঘ্ন হওয়ার পর মুসলমানরা বিজ্ঞান চর্চায় নিমগ্ন হয়।।
অন্যান্য বিজ্ঞানের মত এই বিজ্ঞানেরও ধারাবাহিক শিক্ষা শুরু হয় অষ্টম শতাব্দীর দ্বিতীয় অর্ধে দ্বিতীয় আব্বাসী খলিফা আল্ মনসুরের (৭৫৪-৭৭৫) সময় থেকে। এই সময় গণিত শাস্ত্রের অগ্রগতি একমাত্র মুসলমানগণই দেখিয়েছিলেন। এক্ষেত্রে অবশ্য তারা ভারতীয় এবং গ্রীকদের কাছ হতে কিছু অনুপ্রেরণা লাভ করেছিলেন। যা পরবর্তীকালে আরবীতে অনূদিত হয়েছিল। এই অনুসন্ধান কার্য একাদশ শতাব্দীর শেষ দিক পর্যন্ত সুদূরপ্রসারী হয়েছিল এবং মুসলমানগণই বিশেষ করে গণিতের প্রকৃত সৃষ্টিমূলক কর্ম সম্পাদন করেছিল—তাকে উন্নতির চরম শিখরে পৌঁছে দিয়েছিল। দ্বাদশ শতাব্দীতে খ্রিস্টান এবং ইহুদীগণ ঐ সমস্ত কর্মের অনুবাদ আরবী থেকে ল্যাটিন ও হিব্রু ভাষায় সম্পাদন করে এবং একই সঙ্গে গবেষণামূলক কাজ চালিয়ে যেতে থাকে। তবে ত্রয়ােদশ শতাব্দী পর্যন্ত মুসলমান গণিতজ্ঞগণ অধ্যবসায় দ্বারা যা লাভ করেছিল, তা খ্রিস্টান ও ইহুদীদের কাজের চেয়ে অধিক উন্নত বলে বিবেচিত হয়।
আব্বাসী খলিফা আল্ মনসুরের রাজত্বকাল ছিল মুসলিম বিশ্বের জন্য বিশেষত বিজ্ঞান চর্চার জন্য খুবই গুরুত্বপূর্ণ সময়। ধর্ম-বর্ণ নিবিশেষে অনেক বিজ্ঞানী ও চিন্তাবিদ তাঁর রাজসভা অলংকৃত করেছিলেন। এঁদের একজন ছিলেন আবু ইসহাক আল ফাজারী। ভারতের জ্ঞান-বিজ্ঞান সম্পর্কে তিনিই প্রথম মুসলিম বিজ্ঞানীদের দৃষ্টি আকর্ষণ করেন। ফলিত জ্যোতিষশাস্ত্রে তার চিন্তাধারা ছিল খুব উচ্চাঙ্গের। জানা যায়, তিনিই সর্বপ্রথম মুসলমানদের মধ্যে সূর্য ও নক্ষত্রসমূহের উচ্চতা নির্ণায়ক যন্ত্র আস্তারলব নির্মাণ করেন এবং অংকশাস্ত্রের অন্যান্য যন্ত্রপাতি সম্বন্ধে পুস্তক প্রণয়ন করেন। গণিত বিষয়ে তাঁর প্রণীত গ্রন্থ এখনও অনেক বিষয়ে প্রামাণ্য হিসাবে গৃহীত হয়ে থাকে। আল ফাজারী প্রথম আরব গণনা পদ্ধতি সুনিয়ন্ত্রিত করে আরব বর্ষগণনা ও দিনপঞ্জী প্রণয়ন করেন। ভারতের তৎকালীন বিজ্ঞানী কঙ্কায়ন বা মঙ্ককে ‘সিহিন্দ’ নামক গ্রন্থসহ তিনি মনসুরের দরবারে আনেন। ফাজারী ৭৭৭ সালে মৃত্যুবরণ করেন। আল ফাজরীর পুত্র আবু আবদুল্লাহ মােহাম্মদ ইবনে ইব্রাহীম পিতার উত্তরাধিকারের অংশীদার হয়েছিলেন। তিনি উক্ত ‘সিহিন্দ’ গ্রন্থটি খলিফার আদেশে ৭৭২/৭৩ সালে আরবিতে অনুবাদ করেন। তার এ অনুবাদের উপর ভিত্তি করেই আল খােয়ারিজমী তার বিখ্যাত জ্যোতির্বিজ্ঞান তালিকা ‘ফিল-জিজ’ প্রণয়ন করেন। আবু ইয়াহিয়া আল বাতরিক বিশুদ্ধ গণিত চর্চাতে অবদান রাখেন। তিনি গ্রীক বিজ্ঞানী টলেমীর ‘Tetrabiblos’ গ্রন্থ আরবিতে অনুবাদ করেন।
প্রথম যুগের মুসলিম গণিত চর্চার বিষয় ভারতীয় ও গ্রীক অনুবাদের মধ্যে অনেকটা সীমাবদ্ধ ছিল। গ্রীক জ্ঞান-বিজ্ঞানের উত্তরাধিকার মুসলিম আমলে আরবী অনুবাদের ফলেই ধ্বংসের হাত হতে রক্ষা পায় এবং ইউরােপে প্রচার লাভ করে। H A Salmon is ‘Rise and fall of the Arab Dominion’ গ্রন্থে বলেন,
“The Arab were the first to introduce Greek writers to the notice of the world. They kindled the lamp of learning which illuminated the dark pages of history and it may be safely assumed that were it not for the Arabs, it would have seen long before Europe, the present centre of civilisation and progress would have been irradiated by the bright light of knowledge.”
শুধু তাই নয়, ভারতীয় বিজ্ঞানও আরবদের অনুবাদের কল্যাণে ইউরােপের হাতে পৌঁছেছিল। আজ গণিতের ইতিহাস যে ইউক্লিডের উল্লেখ ছাড়া অসম্পূর্ণ সেই ইউক্লিডকে বিস্মৃতির হাত থেকে রক্ষা করে আধুনিক সভ্যতার লাইম লাইটে নিয়ে আসেন মুসলিম অনুবাদকরা। খলিফা হারুনুর রশীদের (৭৮৬-৮০৯) রাজত্বকালে হাজ্জাজ ইবনে ইউসুফ ইউক্লিড জ্যামিতির প্রথম ৬টি খন্ড আরবীতে অনুবাদ করেন। মামুনের রাত্বকালে (৮১৩-৮৩৩) এ কাজ সমাপ্ত হয়। এখানে উল্লেখ করা প্রয়েজন যে, জ্যোতির্বিজ্ঞানের হাত ধরেই বিশুদ্ধ গণিত চর্চায় মুসলমানরা এগিয়ে আসেন। মুসলিম গণিতজ্ঞদের মধ্যে প্রায় সবাই জ্যোতির্বিজ্ঞানী হিসাবে খ্যাতি লাভ করেন এবং এ বিষয়ে তাদের অনেকগুলাে রচনাও রয়েছে।
আল-মামুনের আমলে জ্যোতির্বিজ্ঞান চর্চায় অনেক উন্নতি অর্জিত হয়। বিভিন্ন স্থানে মানমন্দির স্থাপিত হয়। এ সময় পদার্থবিদ আবুল হাসান দূরবীক্ষণ যন্ত্র আবিষ্কার করেন। বিষুবরেখা ও আয়নমন্ডলের সংযােগস্থল, চন্দ্রগ্রহণ, সূর্যগ্রহণ, ধূমকেতুর ছায়া প্রভৃতি সৌরজগৎ সংক্রান্ত অনেক তথ্যও নির্ণীত হয় এ সময়। আবু আলী ইয়াহিয়া (মৃত্যু ৮৩১খ্রী:), হানে ইবনে আলী (মৃত্যু.৯০০খ্রী.), ওমর ইবনে ফার খান আততাবারী (মৃত্যু ৮১৫ খ্র.), তাঁর পুত্র মােহাম্মদ আবুবকর, আহমদ ইবনে মােহাম্মদ নাহাওয়ান্দী (মৃত্যু ৮৩৫ খ্রী.?), আল মারওয়ারেজী, আল আস্তারলবী, আবুল খায়রাত (মৃত্যু, ৮৩৫খ্রী.) আল ফারগানী এ সময়কার শীর্ষস্থানীয় বিজ্ঞানী ছিলেন।
আল ফারগানী ইউরােপীয়ানদের কল্যাণে যিনি ‘আল ফ্রাগানাস’ নামেই বেশী পরিচিত জ্যোতির্বিজ্ঞান চর্চায় বিশেষ অবদান রাখেন। গণিতের এ শাখায় তাঁর অবদান সম্পর্কে এতটুকু বলাই যথেষ্ট যে, তাঁর প্রণীত ‘Elements of Astronomy’ গ্রন্থটি প্রাচ্যে নিকট অতীত পর্যন্ত ক্লাসিক গ্রন্থের মর্যাদাপ্রাপ্ত হয়েছিল। এটি ‘Gerard of Cremona’ এবং জোহাসে দ্য। লুনা-হিসপ্যালেনসিস কর্তৃক ল্যাটিনে অনূদিত হয়। ইউরােপীয় রেনেসাঁর যুগে রিজিওমন্টানাস এ অনুবাদ পড়ে মুগ্ধ হন এবং ১৪৯৩ সালে মিলানচন দ্যা গ্রেট উক্ত অনুবাদ এর উপর ভিত্তি করে নিউরেমবার্গ থেকে জ্যোতির্বিজ্ঞানের উপর একটি গ্রন্থ প্রকাশ করেন। ১৫৪৬ সালে অ্যানাটোল কর্তৃক এটি পুনঃঅনূদিত হয়ে প্যারিস থেকে বের হয়। এরপরও অনেক ভাষায় এটির অনুবাদ প্রকাশিত হয়। আল্ ফারগানীর ‘জামে এলমুন নুজুম ওয়াল হরকাত আল সামায়িয়া’ (বুক অন সিলেসট্রাল মােসানস অ্যান্ড দ্যা কমটি সায়েন্স অফ দ্যা স্টারস) নামক গ্রন্থটি জ্যোতির্বিজ্ঞানের প্রামাণ্য গ্রন্থ হিসাবে আজও পরিচিত। আস্তারলব সম্বন্ধে তার দুটি গ্রন্থ ‘আল কামিল ফিল আস্তারলব’ এবং ‘ফি সানাত আল আস্তারলব বিল হান্দাসা’ (জ্যামিতির সাহায্যে আস্তারলব প্রণয়ন)-র আরবী অনুলিপি আজও প্যারিস ও বার্লিনে বর্তমান আছে।
আল ফারগানী পরবর্তী সময়কালে গণিতে সমৃদ্ধির যুগ শুরু হয়। বিশেষ করে এ সময়ে আবু মুসা আল খােয়ারিজমীর (৮৪৭) আবির্ভাব নিঃসন্দেহে এক গুরুত্বপূর্ণ ঘটনা। গ্রীক ও ভারতীয় গাণিতিক চিন্তাধারার অনুসৃতির বিপরীতে মুসলিম চিন্তাধারার নতুন যুগ-সংযােজন ঘটে। কালের পাতায় সংযুক্ত হয় নবতর অধ্যায়। আমীর আলী লিখেছেন, উচ্চতর গণিতের প্রত্যেকটি শাখাই মুসলিম প্রতিভার চিহ্ন বহন করে। গ্রীকরা বীজগণিত আবিষ্কার করেছে বলে বলা হয়, কিন্তু যেমন ওলসনার যথার্থই বলেছেন, গ্রীকদের বীজগণিত সীমাবদ্ধ ছিল ‘গবলেট’ খেলার জন্য আমােদের উপকরণ হিসাবে। মুসলমানরা উচ্চতর উদ্দেশ্যে এর ব্যবহার করে আর এইরূপে এর একটি অজ্ঞাতপূর্ব মূল্য সৃষ্টি হয়। আল-মামুনের সময়ে মুসলমানরা দ্বিতীয় পর্যায়ের সমীকরণ আবিষ্কার করে আর অনতিকালের মধ্যে দ্বিঘাত সমীকরণ আর দ্বিপদ উপপাদ্য সৃষ্টি করে। বীজগণিত, জ্যামিতি আর পাটীগণিতই নয়, মুসলমানরা আলােকবিদ্যা আর যন্ত্রবিদ্যারও অসাধারণ উন্নতি সাধন করে। … তারাই সর্বপ্রথম জ্যামিতিতে বীজগণিতের প্রয়ােগ করে, স্পর্শক আবিষ্কার করে আর ত্রিকোণমিতির হিসাবে জ্যা-এর পরিবর্তে ‘সাইন’-এর প্রবর্তন করে। গাণিত্যিক ভূগােলেও তাদের উন্নতি সাধন কম উল্লেখযােগ্য নয়।
আল খােয়ারিজমী গণিত শাস্ত্রে একজন কালজয়ী প্রতিভা। ভারত এবং গ্রীক বীজগণিতের সীমিত চর্চা বাদ দিলে বীজগণিতের যে অবস্থা ছিল তাতে বিশ্বের তেমন কোন মনযােগ ছিল না। আল খােয়ারিজমীই সর্বপ্রথম বীজগণিতকে অঙ্কশাস্ত্রের মধ্যে মর্যাদাসম্পন্ন করে তােলেন। এ জন্য তাকে আধুনিক বীজগণিতের জনক বলা হয়। তার অসামান্য প্রতিভা সম্পর্কে Sarton লিখেছেন,
“The greatest Mathematician of the time, and if one takes all circumstance into account, one of the greatest of all time was Al-Khwarizami?”
পারস্যের খিভা প্রদেশের খারিজমে আল খােয়ারিজমীর জন্মগ্রহণ করেন। তাঁর জীবনী সম্পর্কে তেমন কিছু জানা যায়না। তিনি খলিফা মামুনের লাইব্রেরীর প্রধান লাইব্রেরীয়ান ছিলেন। গণিতের প্রায় প্রত্যেকটি শাখায় খােয়ারিজমীর অবদান রয়েছে। তবে বীজগণিতই তার সর্বশ্রেষ্ঠ দান। জ্যোতির্বিজ্ঞান সংক্রান্ত তার একাধিক গ্রন্থ রেফারেন্সের মর্যাদা লাভ করেছিল উচ্চতা পরিমাপক যন্ত্র, খগােল তালিকা, ডায়াল প্রভৃতি প্রস্তুতকরণে তার অদ্ভুত ক্ষমতার পরিচয় পাওয়া যায়। শুদ্ধ গণিতে তিনি ‘আল জাম্ ওয়াত্ তাফরিক’ গ্রন্থ রচনা করে যে প্রভাব বিস্তার করেন তা ইউরােপীয় ভাষায় এটির বহুবার অনূদিত হওয়ার ঘটনা থেকেই অনুমান করা যায়। Robert of Chester এবং Adelard এই দুই জন আল খােয়ারিজমীর গণিত বিষয়ক গ্রন্থগুলির ল্যাটিন অনুবাদক হিসাবে খ্যাতির অধিকারী হয়ে রয়েছেন। রবার্ট খােয়ারিজমীর শ্রেষ্ঠ অবদান ‘আল হিসাব আলজাবর ওয়াল মুকাবেলা’-র (দ্যা ক্যালকুলেশন অফ ইন্টাগ্রেসন অ্যান্ড ইকুয়েশান) ল্যাটিন অনুবাদ করেন। ১৯১৫ সালে Karpinski নিউইয়র্ক থেকে তা পুনঃ প্রকাশ করেছেন। ১৮৫৭ সালে রােম থেকে Prince Boncompegni কর্তৃক ল্যাটিনে অনূদিত হয় গণিত পুস্তক আল জাম ওয়াত্ তাফরিক -যার নাম দাঁড়ায় ‘Algoritmi denumero Indorum’। ইউরােপীয় ভাষার কবলে পড়ে আরও অনেক মুসলিম বিজ্ঞানীদের মতাে আল খােয়ারিজমীর নাম হয়ে দাঁড়ায় আলগরিদম। বীজগণিতের অন্যতম অংশ লগারিদম যে আজ আমরা দেখতে পাই তা আল খােয়ারিজমী নাম থেকেই উদ্ভূত এবং Algorism, Augrim শব্দগুলােও একই ব্যাপার।

বর্তমান যুগে বিশ্বের সর্বত্র যে অ্যালজেবরা-এর বই পঠিত ও ব্যবহৃত হচ্ছে তা মূলত ‘আল জাবর’ থেকে এসেছে। খােয়ারিজমীর এই বইটি এত বিখ্যাত ছিল যে, ইউরােপের বিশ্ববিদ্যালয়সমূহে গণিত বিভাগে বইটি গণিতের রূপরেখা ও সমাধান দিয়েছে। পি কে হিট্টি বলেন,
“Translated in the twelfth Century into Latin by Gerard of Cremona, this work of Al-Khawarizmi was used until the sixteenth century as the principal mathematical text-book of European universities and to introduce into Europe the science of Algebra, and with it the name.”
অর্থাৎ “দ্বাদশ শতাব্দীতে ক্রোমােনার জেরার্ড ল্যাটিন ভাষায় এই বইটির অনুবাদ করেন। তখন থেকে ষােড়শ শতাব্দী পর্যন্ত ইউরােপের বিবিদ্যালয়গুলােতে এই বইটি গণিত শাস্ত্রের প্রধান পাঠ্যবইরূপে ব্যবহার করা হত। আল খােয়ারিজমীর লেখা এই বইটি ইউরােপে বীজগণিতের প্রচলন করে। এমন কি ‘বীজগণিত নামটি এই বইটির মাধ্যমেই চালু হয়।”
‘কিতাব সুরাত আল আরদ’ (পৃথিবীর ছাদ) তার তৃতীয় পুস্তক। এই বইটি টলেমির ভৌগােলিক পাণ্ডিত্যের উপর ভিত্তি করেই লিখিত এবং সেই সময়কার জানা পৃথিবীর দুটি স্থানের সঠিক দূরত্ব নির্ণয়ে আরও নিখুঁত মাপ দিয়েছিলেন আল খােয়ারিজমী। ভূমধ্যসাগরের সঠিক মাপ এবং আফ্রিকা ও এশিয়ার শহরগুলির অবস্থান ও সঠিক দূরত্ব তিনি নির্ণয় করেন। তিনি আল মামুনের জন্যে বির্ণের মানচিত্র তৈরি করেন এবং ইরাকের সানজার প্রদেশের উপর মধ্যরেখা কল্পনা করে পৃথিবীর ব্যাস মাপার একটি কর্মশালায় অংশগ্রহণ করেন, তার আগে পর্যন্ত জানা ছিল ব্যাস গােলাকার। তিনি ভারতীয় (৭৭০ খ্রীস্টাব্দ) ও গ্রীক তথ্যের উপর নির্ভর করে জ্যোতির্বিজ্ঞানের সারণী (সিন্দহিন্দ জিজ) আঁকেন এবং এখানেই sine 150০-র মান নির্ণয় করেন।
গণিত শাস্ত্রের শূন্য বা ‘Zero’ আল খােয়ারিজমী আবিষ্কার করেন। H G Wells তাঁর ‘The outline of History’ গ্রন্থে আল খােয়ারিজমীকেই শূন্যের আবিষ্কারক হিসেবে পরিচিহ্নত করেছেন। যদিও অনেকেই দাবী করে থাকেন যে, ভারতীয়রাই শূন্যের আবিষ্কারক কিন্তু এর সার্থক ও সফল প্রয়ােগের জন্য আল খােয়ারিজমীই শূন্যের আবিষ্কারক হিসেবে বিশ্ববাসীর কাছে নন্দিত হয়ে আছেন। H.G, wells বলেন,
“The Zero, it is stated, was unknown until the ninth century, When it was invented by a Muslim Mathematician named Muhammadibn-Musa, Who also was the first to use the decimal rotation and who gave the digits the value of position… The Arabs developed spherical trigonometry, inventing the sine, tangent and contangent”
অর্থাৎ “মুহাম্মদ বিন মুসা (আল খােয়ারিজমী) নামে একজন মুসলিম গণিতবিদ কর্তৃক শূন্য আবিষ্কারের পূর্বে নবম শতাব্দী পর্যন্ত শূন্য অপরিচিত ছিল এবং তিনি প্রথম দশমিক চিহ্ন ব্যবহার এবং সংখ্যার স্থানীয় মান নির্ণয় করেন। আরবরা গােলাকার ত্রিকোণমিতির উন্নতি সাধন করেন, সাইন, স্পর্শক এবং কোণ পুরকের স্পর্শরেখা (কোট্যানজেনট) আবিষ্কার করেন।”
আল খােয়ারিজমী প্রথম শূন্যসহ অন্যান্য সংখ্যার ব্যবহার করেন। খােয়ারিজমীর মাধ্যমেই ইউরােপবাসীরা শূন্যের ব্যবহার শিখেছেন। প্রাচ্যের জনৈক আধুনিক পণ্ডিতের মতে,
“খােয়ারিজমীর বীজগণিতের অনুবাদ রবার্ট ল্যাটিন ভাষায় করেছেন। এর গুরুত্বকে অতিরঞ্জিত করা যায় না। কারণ এটাই ইউরােপীয় বীজগণিতের ইতিহাসে নবযুগের সূচনা করেছিল।”
অধ্যাপক রােম লেণ্ডাও বলেন,
“He invents a Modern Algebra, transforms numbers into elements of relation.”
তৎকালীন বিশেষজ্ঞরা খােয়ারিজমীর চিন্তা-চেতনা দ্বারা প্রভাবিত হয়েছিলেন। খােয়ারিজমী অষ্টম শতাব্দীতে ‘Equation of second degree’ আবিষ্কার করেন। আর ডেকার্টে ৫০০ বছর পর তাঁর দ্বারা ব্যবহারিক জ্যামিতি পাশ্চাত্য জগতে পেশ করেন। যারা খােয়ারিজমীর চিন্তা দ্বারা প্রভাবিত হয়েছিলেন তাঁদের মধ্যে মাস্টার জ্যাকব ১৩০৭ সালে অংকশাস্ত্রের ওপর ইতালিয় ভাষায় একটি প্রবন্ধ লিখেছিলেন। এই প্রবন্ধটিতে তিনি ছয় ধরনের দ্বিঘাত সমীকরণ নিয়ে আলােচনা করেছেন। গণিত শাস্ত্রে আল খােয়ারিজমীর অবদানের কথা স্বীকার করতে গিয়ে হিট্টি বলেন,
“Apart from compiling the oldest astronomical tables, Al-Khawarizmi composed the work on Arithmetic, known only in a translation, and the oldest work on Algebra.”
সংখ্যাতত্ত্বে শূন্যের ব্যবহার হঠাৎ করে মিশরে প্রথম হয়েছিল, তবে তা তারা সংখ্যার মাঝখানে বসাতেন, শেষে বসানাের ব্যাপারে অজ্ঞ ছিলেন। আবাকাস আবিষ্কারের পর চিনে শূন্যের ব্যবহার শুরু হয় ইঙ্গিতে, মায়া সভ্যতায় শূন্যের ব্যবহার জানা থাকলেও তাদের স্থির সংখ্যাতত্ত্বই জানা ছিল না। সংখ্যাতত্ত্ব আরবে প্রচলিত হয় সপ্তম শতাব্দীতে, দশম শতাব্দীতে (৯৭৬) গারবার্ট (পরে পােপ সিলভেস্টার-১) আরবী সংখ্যা, (০) শূন্যের ব্যবহার ইউরােপে প্রচলন করেন। খােয়ারিজমী উদ্ভাবিত ১০ ভিত্তিক সংখ্যাতত্ত্ব তথা আলগরিদম সংখ্যাগুলি (১১, ১০১, ১০০১) পরিবর্তিত হয়েছে শুধুমাত্র ০-এর ব্যবহারের উপর নির্ভর করে। ১ থেকে ৯-র সঙ্গে ০ ব্যবহার করে যাবতীয় সংখ্যা লেখা যায়।
আল খােয়ারিজমী নিজস্ব ভাষায় গণিত শিক্ষার প্রয়ােজনীতা সম্বন্ধে বলেন,
“অঙ্কের সহজতম এবং ব্যবহার্য দিক হল, মানুষের নিরবিচ্ছিন্নভাবে প্রয়ােজন হয় জমির উত্তরাধিকার, উইল তৈরিতে, ভাগ-বাঁটোয়ারায়, মামলা-মােকদ্দমায়, ব্যবসায়, পারস্পরিক লেনদেনে অথবা জমির মাপজোকে, খাল কাটতে, জ্যামিত্যিক হিসাব-নিকাশে এবং অন্যান্য নানান ক্ষেত্র।”
তাই ‘আল জাবর’ বইটিতে শুধুমাত্র বীজগণিত নয় অন্য অনেক গণিত বিষয়ে আলােচনা করা হয়েছে। বইটির প্রথম অংশেই শুধুমাত্র বীজগণিতের ব্যবহারিক দিক নিয়ে আলােচনা করা হয়েছে। স্বাভাবিক সংখ্যাগুলির (০ থেকে ৯) ব্যবহার সম্বন্ধে তিনি বলেছেন,
“যখন আমি ভাবি সাধারণ লােকের অঙ্কের ভীতি সম্বন্ধে, আমি দেখেছি এটা পুরােপুরি সংখ্যার জন্যে। আমি আরও দেখেছি, প্রতিটি সংখ্যা কয়েকটি একক নিয়ে গঠিত এবং প্রতিটি একক দিয়ে সংখ্যাটিকে ভাগ করা যায়। আমি আরও লক্ষ করেছি, প্রতিটি সংখ্যা প্রকাশ করা যায় ১ থেকে ১০ পর্যন্ত অঙ্ক দিয়ে। পূর্ববর্তী অঙ্কের সঙ্গে এক একক যােগ করে পরবর্তী অঙ্ক প্রকাশ করা যায়। এরপর ১০-কে দ্বিগুণ ও ত্রিগুণ করা যায় এককগুলির গুণিতক করে, এইভাবে ২০,৩০ করা যায় এমনকি ১০০ এরপর ১০০কে দ্বিগুণ-ত্রিগুণ করা যায় ১০০০ পর্যন্ত, ১০-র সাথে বিভিন্ন একক গুণ করে কিম্বা এরপরেও সবথেকে শেষ সংখ্যা পর্যন্ত।”
আল খােয়ারিজমী এই গ্রন্থে সংখ্যার উৎপত্তি নিয়ে আলােচনা করেন। ভারতীয় সংখ্যা পদ্ধতির অনুসরণ করে তিনি বর্তমানে প্রচলিত বিজ্ঞানসম্মত সংখ্যা লিখন প্রণালী আবিষ্কার করেন। প্রখ্যাত গবেষক এম আকবর আলী জানিয়েছেন-
“আরবদের সংখ্যা লিখন প্রণালী দেখে মনে হয় তারা এই লিখন প্রণালী যেখানেই শিখে থাকুন না কেন সংখ্যার গঠনপ্রণালী তাদের নিজস্ব ও মৌলিক। অন্যগুলির কথা বাদ দিলেও আরব বৈজ্ঞানিকগণ যে অঙ্ক সংখ্যা লিখার মধ্যে শূন্য’ ব্যবহার করবার নিয়ম পদ্ধতির আবিষ্কারক এবং সর্বপ্রথম ব্যবহারকারী সে বিষয়ে সন্দেহ করবার কোন কারণই দেখা যায় না। অনেকের মতে আরবরাই শূন্য’-এরও আবিষ্কারক। তাদের কাছ থেকেই ভারতবর্ষেও ‘শূন্য’র আমদানী হয়।…’শূন্য’ ব্যবহার করবার এবং অঙ্কের সংখ্যা লিখার মধ্যে এর প্রয়ােজনীয়তা আবিষ্কার হওয়ার পূর্বে সংখ্যা লিখন প্রণালী যে জবরজঙ্গ গােছের ছিলাে সে অনুমান করা বিশেষ কঠিন নয়।…শূন্য আবিষ্কারের পূর্ব পর্যন্ত সর্বত্রই এবাকাস ব্যবহৃত হত। রােমের বৈজ্ঞানিক যুগ থেকে আরম্ভ করে একাদশ শতাব্দীর শেষভাগ পর্যন্ত ইউরােপের সর্বত্রই এই অর্ধ বৈজ্ঞানিক প্রণালীতে সংখ্যা-লিখার নিয়ম প্রচলিত দেখা যায়। মধ্যযুগেও যে ইউরােপ বর্তমানের সুষ্ঠ বৈজ্ঞানিক প্রণালীর সঙ্গে পরিচিত ছিলাে এমন মনে করবার কোনাে কারণ নাই। রােম সভ্যতা নির্বাপিত হওয়ার পরে এবাকাস-এর কথাও ইউরােপ সম্পূর্ণরূপে ভুলে যায়। দশম শতাব্দীতে বৈজ্ঞানিক গারবার্ট পুনরায় এই অর্ধ-বৈজ্ঞানিক প্রথা প্রচলন করেন, তার সাথে স্পেনের মুসলিম বৈজ্ঞানিকদের জ্ঞান-বিজ্ঞানের সামান্যতম অংশবিশেষের সঙ্গে পরিচয়ের ফলে। তবে Zero বা ‘শূন্য’ সম্পর্কে তার জ্ঞান একেবারেই শূন্য ছিলাে। ইউরােপে শূন্যর প্রচলন দেখা যায় দ্বাদশ শতাব্দীর প্রথম ভাগে। দ্বাদশ শতাব্দীতেই এর পূর্ণ ব্যবহার করে সংখ্যা লিখন প্রণালী আরম্ভ হয়। এ প্রথাকে আরবদের উৎপত্তি হিসাবে ‘আল্ গরিথম’ বলা হােত। আল খােয়ারিজমীর সময় থেকেই যে শূন্যের ব্যবহার চলে আসছে তার উল্লেখ পাওয়া যায় দশম শতাব্দীতে ইউসুফ প্রণীত ‘মাফাতিহুল উলুম’ (বিজ্ঞান কুঞ্জী’) গ্রন্থে।”
‘আল জাবর আল হিসাব ওয়াল মুকাবেলা’—এটি ল্যাটিনে ‘Ludus algebra almucrgrabalaeque’, ‘Gbeba Mutabila’ ইত্যাদি নামে, ষােড়শ শতকে ‘Algebra and almachabe’ ইংরেজী নামে, ১৮৩১সালে E. Rosen ‘Algebra of Mahammed Bin Musa’ নামে অনুবাদ করেন। অন্য অনেক অনুবাদের মধ্যে ‘Smith The science of reduction and cancellation’ নামে, Cajori করেছেন ‘Restoration and Reduction’ ইত্যাদি নামে। খােয়ারিজমীর গ্রন্থটিকে সব বিষয়েই বীজগণিতের সর্বপ্রথম ও মধ্যযুগের সর্বশ্রেষ্ঠ গ্রন্থের মর্যাদা দেওয়া হয়েছে।
খােয়ারিজমীর পূর্বে গ্রীক বিজ্ঞানী ডায়ােফ্যান্টাস এবং ভারতবর্ষে বীজগণিতের যে সীমিত চর্চা ছিল তা থেকে তিনি সম্পূর্ণ বেরিয়ে এসেছেন। ভারত ও গ্রীক প্রভাবের উপরে ছাপিয়ে উঠেছে তার মৌলিকতার সিঁড়ি। Cajori, Bossault, Cardan, Wallis প্রমুখ তা স্বীকার করেছেন। আল খােয়ারিজমী তার রচনায় বীজগণিতের সমস্ত সূত্র, নানা প্রকার গাণিতিক সমস্যা ও সমাধান খুব সুশৃংখলভাবে তুলে ধরেছেন। পাঁচ ভাগে বিভক্ত গ্রন্থের প্রথম ভাগে আলােচিত হয়েছে বৈজ্ঞানিক দ্বিতীয় মাত্রা সমীকরণের সমাধানের নিয়ম। তিনি এ সমীকরণকে ৬ ভাগে বিভক্ত করেছেন।
বর্গমূলের সঙ্গে সমান যেমন, ax2 = bx
বর্গ সংখ্যার সঙ্গে সমান ax2 = c
মূল সংখ্যার সঙ্গে সমান bx = C
বর্গ ও মূল মিলিতভাবে সংখ্যার সঙ্গে সমান ax2 + bx = c
বর্গ ও সংখ্যা মিলিতভাবে মূলের সঙ্গে সমান ax2 + c = bx
মূল ও সংখ্যা মিলিতভাবে বর্গের সমান bx + c = x2
এখন প্রশ্ন আরবদের মধ্যে এমন বীজগণিতের উদ্ভব হল কেমন করে? এটা সম্পূর্ণভাবে হিন্দুদের নিকট হতে ধার করা নয়, কারণ রাশিগুলিকে সুবিধামত সমীকরণের একদিক হতে অন্যদিকে অপসারণ করে প্রত্যেক রাশিকে ধনাত্মক করার চেষ্টা হিন্দু বীজগাণিতিকদের মধ্যে দেখা যায় না। তেমন আল খােয়ারিজমীর বীজগণিত ডায়ােফ্যান্টাস প্রমুখ গ্রীক বীজগাণিতিকদের গবেষণা হতেও গৃহীত হয়নি, কারণ ডায়ােফ্যান্টাস দ্বিঘাত সমীকরণের একটি মাত্র মূল লক্ষ করেছিলেন এবং অমূলদ রাশিকে তিনি বরাবরই বাদ দিয়েছেন। সম্পূর্ণভাবে ভারতীয় ও গ্রীক বীজগণিতের উপর নির্ভরশীল না হলেও মূলত এই দুই জাতির বীজগণিতীয় গবেষণা হতে আল খােয়ারিজমী যে প্রেরণা পেয়েছিলেন তা নিশ্চিত।
আল খােয়ারিজমী ছয়টি সম্ভাব্য অবস্থান গণনা করে সমাধানের নিয়মসমূহ প্রদান করেন, এবং বর্ণমালার অক্ষর দিয়ে তিনি নিয়মগুলি প্রমাণ করেন। এ প্রকার সমীকরণের দুটি সমাধান হয় বলে তিনি প্রমাণ পেশ করেছেন। গ্রীকরা শুধু একটি মাত্র সমাধান হয় বলে ধরে নিয়েছিলেন। এটা অত্যন্ত আশ্চর্যজনক যে, যখন দুটি root-ই positive তখন তিনি যে root টি radical-এর negative value থেকে উদ্ভূত সেটিই গ্রহণ করেছেন। গ্রন্থের দ্বিতীয় ভাগে বৈজ্ঞানিক সমীকরণগুলাের জ্যামিতিক প্রমাণ এবং তৃতীয় ভাগে (x+a) ও (x+b) এর গুণফল সম্বন্ধে আলােচনা করেছেন। চতুর্থ ভাগে উল্লেখ করেছেন। যে সকল অঙ্কে অজ্ঞাত সংখ্যা, তার বর্গ, বর্গমূল ইত্যাদি রয়েছে সেগুলির যােগ বিয়ােগ, বর্গমূল বের করার নিয়মসমূহ আর পঞ্চম তথা শেষ পরিচ্ছেদে তিনি কতগুলাে সমস্যার সমাধান করেছেন। লেখক সরল এবং চতুষ্পদী সমীকরণের বিশ্লেষণাত্মক সমাধানও করেছেন। তার এই কাজের ফলে সমীকরণে সদর্থক ও নঙর্থক চিহ্নের প্রচলন ঘটে। তিনি জ্যামিতিক সমস্যার সমাধানে সংখ্যার দ্বারা চতুষ্পদী সমীকরণকে চিত্রিত করেছেন। যথা- x2+10x = 30, যা পরবর্তীকালে প্রায় সকল জ্যামিতিবিদকে প্রভাবিত করেছিল। পিসার লিওনার্দো খােয়ারিজমীর মত ছয় প্রকার চতুষ্পদী সমীকরণের আলােচনা করেছিলেন। তিনি মন্তব্য করেছিলেন যে, আরব গাণিতিক পদ্ধতি পিথাগােরাসের পদ্ধতির চেয়ে উন্নত ছিল।
খােয়ারিজমী বীজগণিতে ঋণাত্মক রাশিদের চিহ্ন বদল করে সমীকরণের একদিক হতে অন্যদিকে নিয়ে যাবার এবং সমচিহ্নবিশিষ্ট রাশিদের যােগ দেওয়ার পদ্ধতির নির্দেশ দেন। আরবি ভাষায় প্রথম পদ্ধতির নাম আলজেবর এবং দ্বিতীয় পদ্ধতির নাম আল মুকাবিলা। উদাহরণস্বরূপ, x2-2x = 5x+6 সমীকরণটি আলজেবর নিয়মে দাঁড়াবে x = 2x+5x +6; এবং আলমুকাবিলার নিয়মে হবে x2 = 7x+6. এমন নিয়মের ভিত্তিতে তিনি একঘাত ও দ্বিঘাত সমীকরণ সমাধানের নির্দেশ দিয়েছেন।
তাই গান্তজু বলেছেন,
“আল খােয়ারিজমীর উদ্ভাবিত অ্যালজেবরা বিজ্ঞানের ভিত্তিপ্রস্তর এবং গােড়ার কথা। সজ্ঞানেই বলা যায় ডায়ােফ্যান্টাসের তুলনায় তিনিই অ্যালজাবরার জনক উপাধি পাওয়ার যােগ্য কারণ তিনিই প্রথম বীজগণিতের প্রাথমিক অবস্থার শিক্ষা দিয়েছিলেন।”
আল খােয়ারিজমীর একটি বৈশিষ্ট্য হল, তিনি সমস্ত সমস্যাগুলােই জ্যামিতিক অঙ্কনের মাধ্যমেই সমাধান দিয়েছেন। চিত্র ও বর্গের সাহায্যে এই আলােচনা তাঁর অগাধ প্রজ্ঞার প্রমাণ বহন করে। ভারতীয় বীজগণিত খােয়ারিজমীর ভিত্তি বলে যারা সন্দেহ প্রকাশ করেন এই পদ্ধতি তাদের জবাবের জন্য যথেষ্ট। ভারতীয় বীজগণিতের সকল কাজ সংখ্যা নিয়ে, জ্যামিতিক অংকনের নামগন্ধও তাতে পাওয়া যায় না। ভারত এবং আরব গণিতের মূল পার্থক্য ধরিয়ে দিয়ে Roder বলেছেন,
“The Hindus were more analytical then the Arabs, less pure geometers ; they had in addition the idea of double sign; they transfer more easily a term from one side of an equation to the other, method with them is thus beginning to generalise. It must however, be recognised that as regards exposition their language, pompous and encumbered by its verse form, has not the clearness, exactness and scientific simplicity of that of the Arabs.”
জ্যামিতিকে বীজগণিতের সমস্যা সমাধানে যেমন ব্যবহার করা হয়েছে, বীজগণিতকে এমনকি শুদ্ধ গণিতকেও জ্যামিতির সমস্যা সমাধানের জন্য টেনে নেওয়া হয়েছে। প্রাচীন গাণিতিকরা পাটিগণিত, বীজগণিত এবং জ্যামিতিকে ভিন্ন ভিন্ন খাতে প্রবাহিত করে নিজেদের অজ্ঞাতসারেই গণিতে-বিজ্ঞানে জাতিভেদ প্রচলন করেছিলেন। আর এ থেকে খােয়ারিজমী প্রমুখ বিজ্ঞানী গণিতকে মুক্ত করেন। ‘Encyclopadia of Islam’ লিখেছে,
“In the use of Arithmetic and Algebra in Geometry and vice versa, the solution of Algebraic problems with the aid of Geometry, the Arabs far outstripped the Greeks as well as the Indians. To the Arabs is due the honour of having recognised and emphasised as an obstacle the strict distinction between arithmetical (discontinuous) and geometrical (continuous) magaitude which had so severely impeded the fruitful development of Mathematics among the Greeks.”
এছাড়া আল খােয়ারিজমী পরিমিতি হিসাবে ত্রিভূজ, চতুর্ভূজ, বৃত্ত, পিরামিড প্রভৃতির ক্ষেত্রফল,আয়তন, পরিধি ইত্যাদি নিরূপণের প্রণালী নিয়েও আলােচনা করেছেন এই ‘আল জাবর’ গ্রন্থে। ক্ষেত্রফল নির্ণয়ে তিনি T-এর ২২/৭ মান গ্রহণ করেন। তার মতে, বৃত্তের ব্যাসকে ২২/৭ দিয়ে গুণ করলে পরিধি পাওয়া যাবে।
শুদ্ধ জ্যামিতির সমতল ও বৃত্ত অংকন সম্পর্কে খােয়ারিজমীর গ্রন্থ ইউরােপের কোন কোন লাইব্রেরীতে বিদ্যমান আছে। জ্যামিতিকে তিনি কত সহজসাধ্য করে তুলেছিলেন তা জানা যায় ‘John Bossault’-এর কথায়। তিনি, ‘A General History of Mathematies (1803)’ গ্রন্থে লিখেছেন,
“Practial Geometry and Astronomy owe the Arabs eternal gratitude for having to Trigonometrical calcutation the simple and the commodious forms which it has at present. They reduced the theory of the resolution of triangles, both rectilinear and spherical, to a small number of easy propositions and by the substitution of sines which they introduced instead of the chords of the double ares employed before , they made abridgements in calculations, of inestimable value to those who had a great number of triangles to resolve these discoveries are embodied chiefly to a geometrician and astronomer of the name Muhammad Ben Musa, the author of a work still extant, entitled of “plane and spherical figures.”
খােয়ারিজমী দ্বারা প্রস্তুত ত্রিকোণমিতির সারণী অ্যাডেলার্ড, জেরার্ড ও রজার বেকন দ্বারা অনুদিত হয়। বিখ্যাত বই ‘Image Mundi’ ১৪১০-এ প্রকাশিত হয়, এখানে খােয়ারিজমীর ত্রিকোণমিতির তত্ত্ব অনুদিত হয়। এখান থেকেই কলম্বাস প্রথম জানতে পারেন যে পৃথিবী ন্যাসপাতি আকারের এবং নিশ্চয় পৃথিবীর অন্য প্রান্তে স্ফীত একটি অংশ আছে, যা তিনি মনস্থ করেন আবিষ্কার করতে। তাই ক্রমারের মতে, ইসলামি ভৌগলিক বিবরণ নতুন পৃথিবী (আমেরিকা) আবিষ্কারের ক্ষেত্রে দাবি করতে পারে।।
মৌলিক চিন্তাধারার ক্ষেত্রে আল খােয়ারিজমীর পর সবচেয়ে বিখ্যাত গণিতবিদ ছিলেন আবু আবদুল্লাহ মােহাম্মদ ইবনে ইসা আল্ মাহানী। আর্কিমিডিসের প্রবর্তিত গােলক সম্পর্কিত গবেষণা তার অমরত্বের জন্য যথেষ্ট ছিল। গােলককে খন্ড খন্ড করা নিয়ে যে পদ্ধতি ও প্রথার প্রচলন তিনি করেন তা অভিনবত্বের দাবীদার। জ্যোতিবিজ্ঞানে তাঁর পান্ডিত্য ছিল অগাধ। গােলক বিষয়ে গবেষণা করতে গিয়েই বীজগাণিতিক ত্রিমাত্রিক সমীকরণের উদ্ভব হয়। তিনি তার সমাধানে ত্রিকোণমিতির চিহ্ন, ত্রিমাত্রিক কোণের sine ব্যবহার করেন। আল মাহানী কনিকের সাহায্যে ত্রিমাত্রিক সমীকরণ সমাধানের চেষ্টা করেন। তিনি এ সমস্যাটি এমন গুরুত্বের সাথে নিয়েছিলেন যে, এই সমীকরণটি আল মাহানী সমীকরণ নামে পরিচিত হয়ে পড়ে। তখনকার অঙ্কশাস্ত্রের যে পরিচয় পাওয়া যায়, তাতে ত্রিমাত্রিক সমীকরণের সম্পাদ্যে ত্রিকোণমিতির সাহায্য নেওয়া ধারণাতীত ছিল বলে মনে করা হয়।
ইউক্লিডের জ্যামিতির ভাষ্য রচনা ছাড়াও মাহানী আর্কিমিডিসের মতবাদকে বিশ্বের সাথে পরিচয় করিয়ে দেন। তার অবদান সম্পর্কে ঐতিহাসিক কে আলী লিখেছেন,
“আল মাহানী আধুনিক বীজগণিতের আবিষ্কর্তা। তিনি ত্রিকোণমিতি, জ্যোতির্বিদ্যা, জ্যামিতি ও ঘন সমীকরণ সম্পর্কে পুস্তক রচনা করেন। সমগ্র অন্তর্বর্তী বৈজ্ঞানিক সমস্যা সমাধানের জন্য তিনি বীজগণিতের ব্যবহার পদ্ধতি প্রদর্শন করেন। তিনি চন্দ্র ও সূর্যগ্রহণের এবং গ্রহ ও নক্ষত্রের সংযােগ সম্পর্কে গবেষণা করেন।”
বিজ্ঞানের ইতিহাসে মুসা ভ্রাতৃত্রয় এক বিরল ও বহুমুখী প্রতিভার অধিকারী ছিলেন। আবুল কাসেম আহমদ, আবু জাফর মােহাম্মদ এবং হাসান ইবনে মুসা বিন শাকীর-এই তিন ভাই বাল্যকালেই পিতাকে হারান। খলিফা আল্ মামুন তাদের লালন পালন ও শিক্ষার ভার নেন। মামুনের শিক্ষা ও বিজ্ঞানের বিশাল কর্মর্যজ্ঞে এক সময় এই তিন ভাই জড়িত হয়ে পড়েন এবং স্বস্ব ক্ষেত্রে নিজেদের প্রতিভার স্বাক্ষর রাখেন। তাদের বিশেষ বৈশিষ্ট্য যে, রচিত সকল গ্রন্থ গবেষণা তিন ভাই অথবা যে কোনও দুই ভাইয়ের নামেই পাওয়া যায়। আবু জাফর মােহাম্মদই প্রতিভার বিচারে সর্বশ্রেষ্ঠ ছিলেন। আর হাসান ইবনে মুসা ছিলেন গণিতবিদ হিসাবে শ্রেষ্ঠ আহমদ ছিলেন যান্ত্রিক ও ব্যবহারিক সমস্যার সমাধানে বিশেষভাবে পারদর্শী।
দ্রাঘিমা ও অক্ষরেখার কেন্দ্রস্থল গ্রীনিচ যখন আবিষ্কৃত হয়নি, তখন ভ্রাতৃত্রয় লােহিত সাগরের তীরে নির্ভুলভাবে ডিগ্রি মেপে পৃথিবীর প্রকৃত আকার ও আয়তন নির্ণয় করেন। পৃথিবীর গােল হওয়ার টলেমীর ধারণা এই তিন ভাই প্রথম কাজে লাগান। জ্যোতির্বিজ্ঞানে ক্রান্তবৃত্তের তীর্যকতা সম্পর্কে আলােচনা তারাই প্রথম করেন। চক্রবাল থেকে চন্দ্রের তুঙ্গত্বের হ্রাস বৃদ্ধি পর্যবেক্ষণ, অপভূ, অনুভূ প্রভৃতি কয়েকটি নতুন আবিষ্কারের ফলে তাদের নাম ইতিহাসে অমর হয়ে আছে। এছাড়া জ্যামিতি, কনিক, পরিমিতি প্রভৃতি বিষয়ে তারা গ্রন্থ প্রণয়ন করেন। সমতলভূমি ও গােলক খন্ডের পরিমাণ সম্বন্ধীয় তাদের পুস্তকগুলি জেরার্ড ‘Liber Trium Eratrum’ নামে ল্যাটিনে অনুবাদ করেন। মুসা ভ্রাতৃত্রয়ের হাতে আধুনিক বলবিজ্ঞান বিজ্ঞান হিসাবে প্রতিষ্ঠা পায়। জ্যামিতিতে কোণকে দ্বিখন্ডিত করার পদ্ধতি উদ্ভাবন করেন ইউক্লিড, কিন্তু কোণকে তিনখন্ড করার জটিল নিয়ম আলােচনা করেন তারাই। Conchoid ব্যবহার করে কোণকে ত্রিখন্ডিত করা সম্ভব কিনা, সে বিষয়ে তাঁরাই প্রথম পথ প্রদর্শক। বাহুর পরিমাণ দিয়ে ত্রিভূজের ক্ষেত্রফল বের করার সূত্রটি তাদের আবিষ্কার। ভ্রাতৃত্রয়ের অন্যান্য গ্রন্থাবলীর মধ্যে ফারস্তুন (‘The book on the balance’), গােলক পরিমাপ সম্বন্ধীয় গ্রন্থ “The book on the measurement of the spher’, দুটি নির্দিষ্ট সংখ্যার মধ্যেকার সমানুপাত নির্ণয় বিষয়ক গ্রন্থ, ‘The book on the determination of mean proprotionals between two given quantities’, শুদ্ধ জ্যামিতি সম্পর্কে ‘The Book of the science of the mensuration of plane and spherical figure’ অন্যতম।
আরব দেশের বিশ্বকোষ সংকলক, বিজ্ঞানী এবং দার্শনিক ছিলেন আবু ইউসুফ ইয়াকুব ইবনে ইসহাক, যিনি আলকিন্দি নামে বিশেষ পরিচিত। তিনি মােট ২৭০টি গ্রন্থ রচনা করেছিলেন, যার মধ্যে বিশেষ কতকগুলি ছিল গণিতের উপর। আলকিলিকে ল্যাটিন ভাষায় ‘আল-কিন্দাস’ বলে ডাকা হত। কেননা, তিনি কিন্দাহ গােত্রীয় ছিলেন। তিনি হিন্দি গণনার উপর চারটি গ্রন্থ রচনা করেছিলেন। আল খােয়ারিজমী এবং আলকিন্দি-র রচনার মধ্য দিয়ে গাণিতিক জ্ঞান পাশ্চাত্যবাসীগণ আয়ত্ত করেন।
নবম শতাব্দীর দ্বিতীয়ার্ধে মুসলমান গণিতজ্ঞগণ অধিক সমৃদ্ধি লাভ করেছিল। তার মধ্যে কেউ কেউ পাটিগণিত, জ্যামিতি এবং অপরাপর কিছু বিষয়ের উপর বিশেষজ্ঞ ছিলেন। কেননা, তারা প্রায় সকলেই জ্যোতির্বিজ্ঞানীও ছিলেন এবং ঐ বিষয়েও তাদের যথেষ্ট পারদর্শিতা ছিল, যার ফলস্বরূপ ত্রিকোণমিতির উপর তাদের পারদর্শিতা লক্ষ্য করা গেছে। এই সময় মুসলমানগণ বিজয়ী প্রসার ও প্রসিদ্ধি লাভ করে, যা সম্ভবত গণিতের বিকাশের ফলেই সম্ভব হয়েছিল। সর্বাপেক্ষা আদি মুসলিম দলিল সাক্ষ দেয় যে, মুসলমানগণ গাণিতিক তারিখ হিসাবে ৮৭৪ এবং ৮৮৮ খ্রিষ্টাব্দকে গ্রহণ করত৷
আল ফাজল ইবনে হাতিম আল নাইরিজি (ল্যাটিন-আনারিতিউ, মৃত ৯২২) আল মুতামি-এর সময় টলেমী এবং ইউক্লিডের উপর কমেন্টারী রচনা করে খ্যাতিলাভ করেছিলেন যা পরবর্তীকালে ল্যালি ভাষায় অনুদিত হয়েছিল। তিনি স্পর্শককে প্রকৃত ত্রিকোণমিতির উপাদান হিসাবে ব্যবহার করেছিলেন।
মৌলিক গবেষণার ক্ষেত্রে সাবিত ইবনে কুরার (৯০১) কাজ বিশেষভাবে উল্লেখযােগ্য। ‘অ্যামিকেবল নাম্বারস’ নামে এক জাতীয় সংখ্যার আবিস্কারের জন্য তিনি বিশেষ খ্যাতি লাভ করেন। এই আবিষ্কার নাকি এক চৈনিক পরিকল্পনা হতে উদ্ভূত। সংখ্যাগুলির বৈশিষ্ট এই যে, এর একটি অপর আর একটি সংখ্যার গুণকের যােগফল। একটি উদাহরণের দ্বারা এটা বােঝানাে সহজ হবে।
মনে করা যাক, p=3.2n_1, q=3.2n-1-1, r = 9.22n_1_1 তিনটি মৌলিক সংখ্যা n অবশ্য একটি পূর্ণ সংখ্যা। তাহলে a=2npq ও b=2nr এমন যুগ্ম অ্যামিকেবল সংখ্যা n-এর মান 2 ধরিলে p, q ও r যথাক্রমে ১১,৫ ও ৭১ হবে এবং a ও b হবে যথাক্রমে ২২০ ও ২৮৪। এমন সংখ্যার পরিকল্পনার বৈজ্ঞানিক গুরুত্ব যে খুব বেশি তা নয়, তবে এতে সাবিতের গাণিতিক দক্ষতা পরিস্ফুট। আল মাজরিতিও এই ধরনের গবেষণা পরে করেছিলেন।
ম্যাজিক স্কোয়ার বা জাদুবর্গ সম্বন্ধে সাবিতের আলােচনা প্রনিধানযােগ্য। এই জাদুবর্গের প্রথম আলােচনা চিন দেশে দেখতে পাওয়া যায়। চৈনিক ভাষায় এর নাম লাে-শু। বিখ্যাত চৈনিক পঞ্চশাস্ত্র আই-কিং-এ জাদুবর্গের আলােচনা আছে। তবে জাদুবর্গের কথা কিভাবে আরবদের নিকট পৌঁছেছিল তা সঠিক জানা যায় না। দ্বিতীয় শতকে আলেকজান্দ্রিয়ার গণিতজ্ঞগণ সম্ভবত জাদুবর্গের কথা জানতেন। চিনের সঙ্গে ভারতের যােগাযােগ ও গাণিতিক ভাবধারার আদান প্রদানের ইতিহাস সুপ্রাচীন। সম্ভবত এই দুই সূত্রের কোন একটি হতে চৈনিক লাে-শু-র কথা আরবীয় গণিতজ্ঞগণ অবগত হয়ে থাকবেন। গণিতে সাবিতের অন্যান্য গবেষণা হল তৃতীয় মাত্রার সমীকরণের সমাধান, প্যারাবােলয়েডের ঘনফল নির্ণয়, একটি কোণকে সমভাবে ত্রিখন্ডিত করা ইত্যাদি।
আল বাত্তানী (৯২৯) Sine-কে গ্রীকদের Chords-এর চেয়ে উন্নত করে ব্যবহার করেন। সূর্য ঘড়ির উপরকার সমতলস্থ এবং উধ্বর্তলস্থ ছায়ার ধারণা হতে তিনি কোট্যানজেন্ট ও ট্যানজেন্টের ধারণায় উপনীত হন। ল্যাটিনে এই সমতলস্থ ছায়ার নাম Umbra extensa ও ঊধ্বর্তলস্থ ছায়ার নাম Umbra versa. সূর্য ঘড়ির ফলককে তিনি ১২ ভাগেভাগ করেন। তার সমসাময়িক আর একজন জ্যোতির্বিজ্ঞানী হাবাস অবশ্য একে ৬০ ভাগে ভাগ করেন। যাইহােক সূর্য ঘড়ির ১২ ভাগের ভিত্তিতে- 122
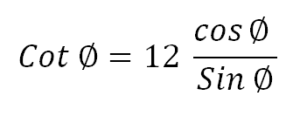
নিয়ম প্রয়ােগ করে আল বাত্তানী কোট্যানজেন্টের এক তালিকা প্রনয়ণ করেন। তারপর সূর্যের উন্নতি নির্ণয়ের উদ্দেশ্যে আমরা তাকে নিচের ত্রিকোণমিতির সূত্র ব্যবহার করতে দেখি—
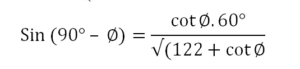
তিনি কোণ ও ত্রিভূজের সঙ্গে অনুভূমিক ত্রিভূজ ও কোণের সম্বন্ধ নিরুপণ করেছিলেন, যা নিম্নলিখিত সূত্র দ্বারা প্রকাশিত –
Cos a = Cos b Cos C +Sin b Sin c Cos A
ইউরােপীয় বিকৃতির ফলস্বরূপ আল বাত্তানী সেখানে Albatenius, Albategnius প্রভৃতি নামে পরিচিত। টলেমীর অনেকগুলাে মতবাদকে তিনি ভ্রান্ত প্রমাণ করেছেন। জ্যোতির্বিজ্ঞানে তালিকা ‘ফিল জিজ’ প্রণয়ন, সৌর অয়নমন্ডলের গতি, চান্দ্র মাসের সঠিক গণনা, নাক্ষত্রিক এবং গ্রীষ্মমন্ডল সংক্রান্ত বৎসরের দৈর্ঘ্য, চান্দ্রিক বিশৃংখলতা, চন্দ্রগ্রহণ, সূর্যগ্রহণ, ঋতুর সঠিক সময় নির্ণয় ইত্যাদি বিষয়ের নতুনতম অবদান বাত্তানীর জ্যোতির্বিজ্ঞান চর্চার বিশেষত্ব।

ত্রিকোণমিতির সম্পূর্ণ স্বাধীন পূর্ণাঙ্গ আলােচনা অঙ্কশাস্ত্রের ইতিহাসে আল বাত্তানীকে অমরতা দান করেছে। ত্রিকোণমিতির যে একটা পূর্ণাঙ্গ স্বাতন্ত্র আছে তা তিনিই প্রথম তুলে ধরেন, তার পূর্বে স্বতন্ত্র বিজ্ঞান হিসাবে ত্রিকোণমিতির কথা ভাবা হতনা। ত্রিকোণমিতির Sine, Cosine, Tangent. Cotangent ইত্যাদি সাংকেতিক নিয়মগুলােকে প্রকৃত তাৎপর্যপূর্ণভাবে ব্যবহার করতে তাঁর পূর্বে কেউই সক্ষম হননি। তিনিই প্রথম এসব সংকেতের মধ্যে সম্পর্ক আবিষ্কার করেন। তার উদ্ভাবিত সূত্রের একটি হল, কোনও কোণের Sine জানা থাকলে তার Tangent বের করা বা Tangent জানা থাকলে Sine বের করা যায় অতি সহজেই।
যে সকল প্রতিপাদ্য বিষয় গ্রীকরা জ্যামিতির সাহায্যে সম্পন্ন করতেন তিনি সেগুলাে বীজগণিতের সাহয্যে সম্পন্ন করেন। তার সব গ্রন্থের সন্ধান পাওয়া যায় না। প্রাপ্ত গ্রন্থের মধ্যে ‘মারফাতে মাতালী আল বুরুজ’, ‘রিসালা ফি তাহকীক আকদার’, ‘আল জিজ’, ‘মাকালাত আরবা লি বাতমিয়াস’ অন্যতম।
আল মাজেস্ট প্রদত্ত গােলকের উপরিভাগে অঙ্কিত ত্রিভূজ সংক্রান্ত সমস্ত সূত্রের সঙ্গে তিনি সম্যকভাবে পরিচিত ছিলেন। ত্রিকোণমিতির এমন উন্নতির ফলে বিজ্ঞানে বিশেষ করে জ্যোতির্বিদ্যায়, উন্নততর গবেষণার পথ যে কেমন সুগম হয়েছিল সে সম্বন্ধে মন্তব্য প্রসঙ্গে কারা দা ভক্স লিখেছেন,
“This brings us very far beyond the point reached by the Greeks and really opens the era the modern science.”
দশম শতাব্দীতে গণিতের সমস্ত কর্ম বিশেষভাবে মুসলমানদের দ্বারা সৃষ্ট হয়েছিল এবং সমস্ত লেখনী ছিল আরবী ভাষায়। এইশতাব্দীর শেষে অগণিত মুসলমান গণিতবিদের আবির্ভাব ঘটেছিল, তাদের মধ্যে আবু কামিল এর নাম বিশেষভাবে উল্লেখযােগ্য। তিনি আল-খােয়ারিজমীর বীজগণিতের উপর অধিক পারদর্শিতা দেখান। তিনি চতুষ্পদী সমীকরণের পুনর্বিন্যাস ও নির্ধারণ প্রক্রিয়ার সমাধান করেছিলেন। তিনি বীজগণিতে পেন্টাগন এবং ডেকাগনের উপর বিশেষজ্ঞতা লাভ করেছিলেন এবং যােগ ও বিয়ােগের সূত্র রচনা করেছিলেন। ‘History of Mathematics’-এ Smith লিখেছেন,
“No writer of his time showed more genius than he is the treatment of equations and their application to the solution of geometric problems.”
শুদ্ধ অংক ও বীজগণিতের উপর তিনি অনেক গ্রন্থ রচনা করেন। বর্তমান ভগ্নাংশ লিখন প্রণালীর যে ব্যবহার তা তিনিই আবিষ্কার করেন। বীজগণিতের দ্বিমাত্রা সমীকরণের উভয় প্রকার সমাধানের ব্যবহার তার সর্বশ্রেষ্ঠ অবদান।
তিনি গুণিতক এবং বীজগণিতের পরিমাণের উপর সমীক্ষা চালিয়ে সমীকরণের পাঁচটি অজানা তথ্য নির্ণয় করেছিলেন। আল কারখি এবং পিসার লিওনার্দো তার গাণিতিক কর্মকে প্রভূত পরিমাণে ব্যবহার করেছিলেন।
চিকিৎসক এবং গাণিতিক আবু উসমন সঈদ ইবনে ইয়াকুব আল দিমাস্কাসী (৯০৪-৯৩২ খৃঃ) খলিফা মুক্তাদিরের সময় বাগদাদে আবির্ভূত হয়েছিলেন। তিনি অ্যারিস্টটলের সূত্র, ইউক্লিড এবং গ্যালেনা-র ‘Temperament’, ‘Pulse’ ইত্যাদির আরবী অনুবাদ করেছিলেন। তাঁর উল্লেখযােগ্য কাজের মধ্যে ইউক্লিডের ‘Book-x’-এর নাম অগ্রগণ্য, যাঁর কমেন্টারী পাপুসএর সহায়তায় লিখিত হয়েছিল। তিনি বাগদাদ, মক্কা এবং মদিনার হাসপাতালের অধ্যক্ষ ছিলেন।
জ্যোতির্বিদ এবং গাণিতিক আবু ইসহাক ইব্রাহিম ইন সিনান সর্বপ্রথম কনিস্ এবং আলমাজেস্ট-এর উপর কমেন্টারী রচনা করেছিলেন। তাছাড়া জ্যামিতি ও জ্যোতির্বিজ্ঞানের উপর তিনি বহু পুস্তক রচনা করেছিলেন। উদাহরণস্বরূপ, সুনডিয়াএর নাম করা যেতে পারে। তার অধিবৃত্ত ও চতুর্ভুজের তত্ত্ব আর্কিমিডিস্ত্রে চেয়েও সরল ছিল এবং প্রকৃতপক্ষে তা ‘Integral Calculus’-এর আবিষ্কারের পূর্বে সরল হিসেবে বিবেচিত হত। ইব্রাহিমের পিতা সিনানও একজন জ্যোতির্বিদ ও গাণিতিক ছিলেন এবং উভয়েই ইসলাম ধর্মগ্রহণ করেছিলেন।
গাণিতিক এবং জ্যোতির্বিদ আলি ইবনে আহমদ আল ইানী (মৃঃ৯৫৫খৃঃ) আবু কামিলের বীজগণিতের উপর কমেন্টারী রচনা করেছিলেন। আবু জাফর আল খাজিন (মৃঃ ৯৬১) ইউক্লিডের ‘দশম গ্রন্থের’ উপর ভাষ্য রচনা করেছিলেন। তাছাড়াও গণিত এবং জ্যোতির্বিজ্ঞানের উপর অনেক কাজ করেছিলেন। তিনি আল মাহানীর সমীকরণের (বিশেষত কনিক সোন এবং কিউবিক ইকুয়েশন) সমাধান করেছিলেন।
আল কুহী গণিত ও জ্যোতির্বিজ্ঞানের উপর অনেক লেখনী রচনা করেছিলেন। জ্যোতির্বিজ্ঞানের তুলনায় গণিতের ক্ষেত্রে তাঁর অবদান বেশি। গ্রীক জ্যামিতির পুনর্জাগরণ ও পরম্পরা চালিয়ে যাওয়ার জন্য ঘন ও Quadratic সমীকরণের সমস্যাগুলি সমাধানে তিনি ব্যাপৃত হন। নাসিরউদ্দিন তুসি আল কুহীর গণিত বিষয়ে আলােচনা করতে গিয়ে বলেছেন,
“একটি বৃত্তের অংশ তৈরী করতে যা অন্য একটি বৃত্তাংশের আয়তনের সমান বা অপর একটি বৃত্তাংশের ক্ষেত্রফলের সমান, আর্কিমিডিস একই ধরনের বা আরও কঠিন সমস্যার সমাধান করেছিলেন। আল কুহী দুটি অজানা দৈর্ঘ্য তৈরি করলেন, একটি সমবাহু অধিবৃত্তকে পরাবলয় দ্বারা ছেদ করে এবং এই অবস্থা বারবার আলােচনা করেছেন।”
ইউক্লিডের ‘এলিমেন্টস’, অ্যাপােলােনিয়াসের ‘কনিকস’ ও আর্কিমিডিসের গােলক ও শঙ্কুর প্রাচীন সমাধানের ফলও তিনি আয়ত্ত সমাধান করেন। আল কুহী ‘তলের শঙ্কুর অবতারণা করেন যা অনেক আলােচনার পর সমাধান করেছেন অধিবৃত্তের উপর অঙ্কিত স্থানাঙ্ক দিয়ে। তারপর দুটি বক্ররেখার। ছেদের মাধ্যমে সমাধান করা হয়েছে। তিনি একটি শাঙ্কব কম্পাস ব্যবহার করেন যার একটি পা বাড়ানাে কমানাে যেত এবং তা দিয়ে শঙ্কুর ছেদ, সরলরেখা, বৃত্ত আঁকা যেত, এছাড়াও অ্যাস্ট্রোল্যাব, সূর্যঘড়ি প্রভৃতি তৈরিতে সাহায্য করত। অ্যাস্ট্রোল্যাব তৈরিতে যে সমস্যার উদ্ভব হয় তা নিয়ে তিনি দুটি বই লেখেন—প্রথমটি চার অধ্যায় যুক্ত, দ্বিতীয়টি সাত অধ্যায় যুক্ত। এই বইয়ে মানচিত্র অঙ্কনের অনেক সমস্যার সমাধান তিনি করেছেন। তিনি গােলকের নিরীয় তলে বৃত্ত আঁকেন।
গাণিতিক আবু সঈদ আহমদ আলসিজ্জি (৯৫১-১০২৪) কনিক সেক্সন এবং সার্কেন্স ইন্টারসেক্সনের উপর বিশেষ চর্চা করেছিলেন। তিনি কোণের পুরাতন কাইনেটিক্যাল ট্রাইসেক্সনকে প্রকৃত জ্যামিত্যিক সমাধান দ্বারা পুনস্থাপন করেছিলেন। অপর এক ব্যক্তি আল সাঘানী (মৃঃ ৯৯০) কোণের অনুচ্ছেদের উপর বিশেষ শিক্ষা লাভ করেছিলেন।
আবুল ওয়াফা ছিলেন তৎকালীন একজন সর্বশ্রেষ্ঠ জ্যোতির্বিদ এবং গাণিতিক। তিনি বাগদাদে জন্মগ্রহণ করেছিলেন এবং সেখানেই ৯৯৭/৯৯৮ খৃঃ মৃত্যুবরণ করেন। তিনি সর্বশেষ গ্রীক তত্ত্বের আরবী অনুবাদক এবং ভাষ্যকার হিসাবে পরিচিত। ইউক্লিড, ডায়ােফ্যান্টাস এবং আল খােয়ারিজমীর তত্ত্বের উপর তিনি কমেন্টারী রচনা করেছিলেন। তাছাড়াও একটা ব্যবহারিক গণিত আমাদের উপহার দিয়েছেন তিনি, যার শিরােনাম হল ‘কিতাব আল কামিল’ (পূর্ণগ্রন্থ)। অপর একটি গ্রন্থ যা প্রায়ােগিক জ্যামিতির উপর লিখিত হয়েছিল, তার নাম দিয়েছিলেন ‘কিতাব আল হানদাসা’। তিনি কম্পাসের সাহায্যে জ্যামিতিক সমস্য সমাধানের পদ্ধতি উদ্ভাবন করেছিলেন। তিনি চতুর্ভুজের গঠন, অপরাপর চতুর্ভুজের সমানুপাতিক বর্ণনা এবং রেগুলার হেপ্টাগণের গঠন আলােচনা করেছিলেন। এছাড়াও তিনি রেগুলার পলিহেড্রন এবং অধিবৃত্তের গঠন নির্ধারণ করে গণিতের অগ্রগতিকে ত্বরান্বিত করেছিলেন। তিনি জ্যামিতিক সমাধান নিম্নলিখিত সূত্র দ্বারা সম্পাদন করেছিলেন—
x4 = a 97 x4 + ax3 = b
ত্রিকোণমিতির ক্ষেত্রে আবুল ওয়াফা-র অবদান শ্রদ্ধার সঙ্গে স্মরণীয়। তিনিই ছিলেন প্রথম ব্যক্তি , যিনি Sine তত্ত্বের সার্বিকতা এবং আনুভুমিক ত্রিভুজের সঙ্গে তার সম্বন্ধ ব্যাখ্যা করেছিলেন। তিনি Sine ছকের একটা নতুন পদ্ধতির উদ্ভাবন করেছিলেন। নতুন পদ্ধতি প্রয়ােগ করে Sine 30° (1/2)-এর মান দশমিকের পর আট ঘর পর্যন্ত শুদ্ধভাবে নির্ণয় করেছিলেন। তিনি আগে থেকেই বলে দিয়েছিলেন বর্তমান যুগের ত্রিকোণমিতির সংজ্ঞা নির্ণয়ের জন্য বৃত্তের একক ব্যাসার্ধ ব্যবহার করা হবে। তিনি ত্রিকোণমিতিতে Secant সংযােজিত করেছিলেন, যা ত্রিকোণমিতির এক মৌলিক উপাদান বলে বিবেচ্য। তাছাড়া তিনি স্পর্শকের উপর বিশেষ শিক্ষাপ্রাপ্ত হয়ে একটা স্পর্শক ছকও তৈরি করেছিলেন। তিনি ত্রিকোণমিতির ছয়টি লাইনের সঙ্গে তার সাধারণ নিয়মের একটা সংযােগ স্থাপন করেছিলেন, যা বর্তমানে ত্রিকোণমিতিকে সংজ্ঞায়িত করার জন্য ব্যবহার করা হয়।

বাত্তানীর হাতে অস্ফুট ত্রিকোণমিতি ওয়াফার হাতে সম্পূর্ণ স্ফুরণের গতি লাভ করে। দুই কোণের Sine-এর সমষ্টি যে Sine ও Cosine দ্বারা নির্ণয় করা যায় তা প্রথম আবুল ওয়াফাই উদ্ভাবন করেন। বর্তমান ত্রিকোণমিতির প্রাথমিক সূত্র Sin (A+B) = Sin A Cos B + Cos A Sin B আবুল ওয়াফার পূর্ব পর্যন্ত কেউ জানত না, এমনকি ষােড়শ শতকের বিখ্যাত বিজ্ঞানী Copernicus পর্যন্ত এ সম্পর্কে অজ্ঞ ছিলেন। (সমরেন্দ্রনাথ সেন, বিজ্ঞানের ইতিহাস, আরব্য বিজ্ঞান অধ্যায়, পৃ. ১৩৬)।
ত্রিকোণমিতির সংজ্ঞা ও নতুন ব্যাখ্যা প্রদান দুই কোণের সমষ্টির সাইন, কোণের অর্ধাংশের সাইনের বর্গের সাথে কোসাইনের সম্বন্ধ, কোণের সাইনের সঙ্গে সেই কোণের অর্ধেকের সাইনের ও কোসাইনের সম্বন্ধ তিনিই প্রথম প্রবর্তন করেন। কাররা দ্য ভক্স আবুল ওয়াফার অবদানের মূল্যায়ন করে বলেছেন, ত্রিকোণমতিতে আবুল ওয়াফার অবদান অবিতর্কিত। তার দ্বারা ত্রিকোণমিতি অধিকতর স্পষ্ট-ভাষিত হয়েছে।
কোপারনিকাসের ছাত্র রায়েটিকাস অনেক পরিশ্রম করে তার ‘অপাস টিনাম দ্য ট্রায়েঙ্গুলিস’ গ্রন্থে আবুল ওয়াফার থেকে জটিলতর আর একটি সূত্র উদ্ভাবন করে পূর্বোক্ত সূত্রটি পুনরাবিষ্কার করেন। আবুল ওয়াফা বৃত্তচাপের জ্যায়ের মূল্য নির্ধারণের পদ্ধতির উপর একটি উত্তম ও উপযােগী পুস্তিকা (ফী ইসতিখরায় আল আউতার) রচনা করেন। তিনি পাটিগণিতের উপর একটি উত্তম পুস্তিকা ‘মানাজিল’ এবং পাটিগণিতের ভূমিকা হিসাবে ‘মুদকিল’ লেখেন।
আবুল ওয়াফার বিজ্ঞানে অবদানের এটি শেষ নয়। এক বিরাট উদ্ভাবনী শক্তির জ্যামিতিবেত্তা হিসাবে তিনি কিছু সংখ্যক সমস্যা নিয়ে মাথা ঘামান। তিনি অধিবৃত্তের সমচতুষ্কোণতা নিয়ে এবং অধিবৃত্তাকার পাত্রের ঘনফল নিয়ে গবেষণা করেন। (সমরেন্দ্র নাথ সেন, পূর্বোক্ত, পৃ. ১৩৬) বীজগণিতে তিনি ডায়ােফ্যান্টাস অনুবাদ করেন এবং এটির উপর বিস্ততৃ টীকা-টিপ্পনি ও মন্তব্য সংযােজন করেন, কিন্তু এই লেখাগুলি হারিয়ে গেছে।
আবুল জুদ একাদশ শতকের প্রথম ভাগের বিজ্ঞানী। তাঁর গবেষণার বিষয় ছিল জ্যামিতি। আবু কামিলের (মৃত্যু ৮৫০) অনুসৃত পথে তিনি বহুভূজের নানা সমস্যা সমাধানের জন্য জ্যামিতি প্রয়ােগ করেন। বহুভূজের মধ্যে সপ্তভূজ ও নবভূজ সংক্রান্ত আলােচনায় তাঁর দৃষ্টি পড়ে এর মধ্যে সুষম সপ্তভূজের বাহুর পরিমাপ নির্ধারণের বিষয়টি বিশেষভাবে উল্লেখযােগ্য। এই নির্ধারণ প্রসঙ্গে প্রয়ােজনীয় x3-x2-2x+1= 0 সমীকরণটি তিনি সমাধান করেন। এটা একটা তৃতীয় মাত্রার সমীকরণ। এর সমাধানের দ্বারা তিনি উপরােক্ত সুষম সপ্তভুজের বাহুর পরিমাপ নির্ধারণে সক্ষম হন। তাঁর দ্বিতীয় উল্লেখযােগ্য গবেষণা হল, কোণকে ত্রিখন্ডিত করা। কণিক জ্যামিতির সাহায্যে তিনি এই সমস্যার সমাধান করেন। একটি অধিবৃত্ত ও সমবাহু পরাবৃত্তের ছেদন দ্বারা এই সমস্যার সমাধান হয়।
আবু মহম্মদ হামিদ আল খােজান্দির (১০০০ খ্রীঃ) প্রসিদ্ধি প্রধানত বীজগাণিতিক গবেষণার জন্য। তিনি নানা প্রকার সমীকরণের সমাধান করেন। তিনিই প্রথম দেখান যে, মূলদ সংখ্যার ধারণা অনুসারে দুটি ত্রিঘাত সংখ্যার যােগফল আর একটি ত্রিঘাত সংখ্যার সমান হতে পারে না। অথাৎ x3+y3 = Z প্রখ্যাত ফরাসী গণিতজ্ঞ ফেরমা এর কথা উল্লেখ করেছেন। তার নাম অনুসারে এটা ফেরমার সর্বশেষ প্রতিপাদ্য নামে পরিচিত। আল খােজান্দির প্রমাণ নিখোঁজ হয়েছে এবং অনেকের মতে, তার প্রমাণে কিছু কিছু ত্রুটি ছিল। x3+y3=z3 সমীকরণের সমাধান যে অসম্ভব, বাহাউদ্দিন নামে আর এক গণিতজ্ঞ সেকথা বলেছিলেন। আল খােজান্দি জ্যোতিষ সম্বন্ধেও কিছু কিছু গবেষণা করেছিলেন। তিনি একটা সেক্সটান্ট তৈরী করে তার সাহায্যে সূর্যের সর্বাধিক উন্নতি নির্ধারণ করেন। তার এক পর্যবেক্ষণ অনুসারে ক্রান্তবৃত্ত ও ভূবিষুববৃত্তের অন্তর্বর্তী কোণের পরিমাণ ২৩° ৩২’২১” নির্ধারিত হয়েছিল। এটাও মনে করা হয় যে, তিনি Sine তত্ত্বের সঙ্গে অনুভূমিক ত্রিকোণের আবিষ্কর্তা।
আবু নসর মনসুর ইবনে আলি, যিনি আলবিরুনীর শিক্ষক ছিলেন, তিনি মেনেলাউসের অনুভুমিক তত্ত্বের উন্নয়ন সাধন করেছিলেন। ত্রিকোণমিতি এবং জ্যোতির্বিজ্ঞানে বহু গ্রন্থের তিনি প্রণেতা ছিলেন। ইবনে আহমদ বাণিজ্যিক গণিতের উপর গ্রন্থ রচনা করেছিলেন যার নাম ‘আল-মুয়ামালাহ’। তিনি ইরােটিক ক্ষমতাকে বহু সংখ্যায় ব্যাখ্যা করেছিলেন।
এরপর আমরা একাদশ শতাব্দীর গাণিতিক উন্নয়ন সম্পর্কে আলােচনায় অগ্রসর হব। এই সময়ের গাণিতিক উন্নয়নে ল্যাটিন ও মুসলমানদের কি ভূমিকা ছিল তা জর্জ সার্টনের লেখনীত প্রকাশ পায় “গাণিতিক জ্ঞান স্বল্পমাত্রায় উপস্থিতি লক্ষ করা যায় ল্যাটিন লেখনীতে, যা ক্রমান্বয়ে বর্ধিত হয়েছিল, কিন্তু তা ত্রয়ােদশ শতাব্দী পর্যন্ত প্রভাব বিস্তার করেনি যতদিন না আরব্য জলের দ্বারা তা “বিত হয়েছিল। তিনি পুনরুল্লেখ করেন যে,
“এরপর ইসলামের জগতে আসা যাক, এটা প্রায় অন্ধকার জগৎ থেকে উন্মুক্ত আলােতে উত্তরণ এবং যা ছিল এক নিদ্রিত জগৎ থেকে চূড়ান্ত কর্মব্যস্ত জগতে পদার্পণ।”
প্রাচ্যের গাণিতিক জ্ঞান ইজিপ্ট, স্পেন, মরক্কো, তিউনিস্ ও অন্যান্য স্থানে বিস্তার লাভ করেছিল। ইবনে ইউনুস (১০০৯ খ্রীঃ) গণিতে একটা সূত্র তৈরী করেছিলেন, যা লগারিদমের পূর্বে অবিচ্ছেদ্য বলে বিবেচ্য ছিল। যেমন—
cos a cos B = 1/2 [cos (a-B) + cos (a+B)]
তিনি আবার তার একটা মােটামুটি মূল্য নির্ধারণ করেছিলেন, যথা—
Sin 1০ =1/3. 8/9 sin (9/8)০ + 2/3. 16/15 sin (15/16)০.
ত্রিকোণমিতির উন্নয়নের উপর অভূতপূর্ব অবদান রেখে গেছেন গাণিতিক কুশায়র ইবনে লাব্বান।
আবু জাফর মহম্মদ ইবনে আল হুসেন, সমকোণী ত্রিভুজের উপর এবং জ্যামিতিক পদ্ধতি বনাম কাইনেটিক পদ্ধতির উপর গ্রন্থ রচনা করেছিলেন, যা পরবর্তীকালে ফরাসী ভাষায় অনূদিত হয়েছিল। একে মুসলমানগণ ‘আন হানদাসা আল সাবিত’, বা ‘অপরিবর্তিত জ্যামিতি’ বলে গণ্য করত। আবু জাফর স্পর্শকের একটি বিশেষ ছকও তৈরি করেছিলেন। তিনি সমীকরণের সমাধান এভাবে করেছিলেনঃ –
X2+a =Y2
আল-কারখী বাগদাদে আবির্ভূত হয়েছিলেন, যখন আবু আল-মুল্ক (-১০১৬) মন্ত্রীপদে বহাল ছিলেন। সমকালে তিনি একজন শ্রেষ্ঠ গাণিতিক হিসাবে গণ্য হয়েছিলেন। পাটিগণিতের উপর তিনি যে গ্রন্থ রচনা করেছিলেন তার নাম ছিল ‘আলকাফি-ফিল-হিসাব’ (গণনার পর্যাপ্ত)। এই গ্রন্থের ভিত্তি অধিকভাবে গ্রীক জ্ঞানের উপর প্রতিষ্ঠিত ছিল। তিনি নিউমেরিক্যালস ব্যবহারের পরিবর্তে ‘নাম্বারস’-এর পূর্ণ মান লিখেছিলেন। বীজগণিতের উপর রচিত পুস্তক তিনি তৎকালীন মন্ত্রীকে উৎসর্গ করেছিলেন। গ্রন্থটির নাম ছিল ‘আলফাখরী।
বীজগণিত বইটিতে আছে অনেক জটিল অঙ্ক এবং অনেক গাণিতিক সমস্যার সমাধান। আলেকজান্দ্রিয়ার ডায়ােফ্যান্টাসের লেখা গােড়ার বীজগণিত পদ্ধতির পরিচয় আছে এই আশ্চর্য বীজগণিত বইটিতে। সংখ্যাতত্ত্ব সম্বন্ধে তার গবেষণা মৌলিক। বীজগণিতে তিনি বহু ক্ষেত্রে ডায়ােফ্যান্টাসকে অনুসরণ করেন এবং তার উদ্ভাবিত পদ্ধতি বিশেষ দক্ষতার সঙ্গে প্রয়ােগ করেন। তিনি উচ্চতর মাত্রার বহু সমীকরণের সমাধানের জন্য বিখ্যাত। এমন এক উচ্চ মাত্রার সমীকরণ হচ্ছে x2n + axn = b. এজাতীয় উচ্চমাত্রার সমীকরণের সমাধানের প্রচেষ্টা তিনিই প্রথম করেন। তারপর দ্বিঘাত সমীকরণের সমাধান তিনি দিতেন জ্যামিতি ও পাটিগণিত উভয় পদ্ধতি অবলম্বনে।
বিভিন্ন শ্রেণীর যােগফল নির্ণয় করার কতকগুলি পদ্ধতি তিনি আবিষ্কার করেন। তার মধ্যে একই শক্তির ক্ষমিক সংখ্যার যােগফল সংক্রান্ত সূত্রগুলি বিশেষভাবে প্রনিধানযােগ্য। উদাহরণস্বরূপ—
12+22+32+ ….+n2=(1+2+3+..3.+n)2n
12+23+33+….+n3 = (1+2+3+….+n)2
সূত্রগুলি এবং তাদের প্রমাণ আল কারখী উদ্ভাবন করেন।
বীজগণিতে আল কারখীর একটি লক্ষণীয় বিষয় এই যে, ভারতীয় গণিতবিদগণ কর্তৃক উদ্ভাবিত অনির্ণেয় সমীকরণের কোনরকম আলােচনা বা উল্লেখ এতে পাওয়া যায় না। তার পাটিগণিত সংক্রান্ত বইটিতে দশমিক স্থানিক অঙ্কপাতন পদ্ধতি ব্যবহৃত হয়নি, সে স্থানে সংখ্যা লিখিত হয়েছে সম্পূর্ণ গ্রীক পদ্ধতি অনুসারে।
প্রখ্যাত ফার্সী গাণিতিক আবুল হাসান আলি আল-নাসাবী, যিনি সুলতান মাজি-আল-দাওলাহ্ (১০২৯ খ্রীঃ)-র সময় সমৃদ্ধি লাভ করেছিলেন এবং তাঁর পৃষ্ঠপােষকতায় ব্যবহারিক গণিতকে ফার্সী ও আরবী ভাষায় অনুবাদ করেছিলেন। তাঁর গণিতকে ‘আল মুঘনি-ফিল-হিসাব-আল-হিন্দি’ বলা হত। তিনি ভগ্নাংশ এবং চতুর্ভুজ ও কিউবিক রুলের বিভাগকে বিশ্লেষণ করেছিলেন। তিনি সেক্সাডেসিম্যালকে ডেসিম্যাল ভগ্নাংশে রূপান্তরিত করে পূর্ণ প্রতিষ্ঠা করেছিলেন, যা এক উল্লেখযােগ্য ঘটনা বলে বিবেচিত হত। উদাহরণ স্বরূপ—
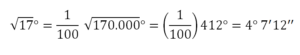
পাশ্চাত্যে আল হাজেন নামে সুপরিচিত আল হাইসাম বিজ্ঞানের এক উজ্জ্বল আলােকবর্তিকা। চশমা আবিষ্কারের জনক। হলেও তিনি পদার্থবিদ্যা, জ্যোতির্বিদ্যা, ও গণিতশাস্ত্রে অমূল্য অবদান রেখেছেন। ইরাকের বসরাতে তিনি ৯৬৫ খৃষ্টাব্দে জন্মগ্রহণ করেন এবং ১০৩৯ খৃষ্টাব্দে মতান্তরে ১০৪৪খৃষ্টাব্দে মত্যুবরণ করেন।

আল হাইসাম অন্যান্য বিষয় ছাড়া, অংকে ৪১টি এবং জ্যামিতিতে ২৬টি গ্রন্থ রচনা করেন। শুদ্ধ অংকশাস্ত্রের মধ্যে জ্যামিতি, কনিক্স, বীজগণিত,গতিবিদ্যা, তরল পদার্থবিজ্ঞানে অবদান তাকে বিশিষ্ট স্থান দান করেছে। পদার্থবিদ্যার সাথে উচ্চমানের গণিতের এক অবিচ্ছিন্ন সম্পর্ক রয়েছে। আল হাইসাম তাই উভয়টি একত্রে আলােচনা করেন। ‘কিতাবুল মুনজিরে’ তিনি যেভাবে জ্যোতির্বিজ্ঞান ও জ্যামিতির ব্যবহার করেছেন তার পূর্বে কেউই তেমনটি করেননি। জ্যামিতিক সমস্যায় গােলাকৃতি প্রতিফলক থেকে আলাের প্রতিফলনের নিয়ম এবং বস্তু ও তার প্রতিকৃতির সম্পর্ক সম্বন্ধে সমস্যাও তার জ্যামিতিক সমাধান। যেমন, একটি বৃত্ত নেওয়া হােক যার কেন্দ্র বিন্দু হল O আর ব্যাসার্ধ হল R, এই বৃত্তে একই সমতলে রয়েছে দুটো বিন্দু A ও B, এখন এই বৃত্তে এমন একটা M বিন্দু বের করতে হবে যেখানে A থেকে আলাে এসে বৃত্ত থেকে প্রতিফলিত হয়ে B বিন্দু দিয়ে যাবে। অন্যভাবে সমস্যা হল, কতগুলাে বিশেষ অবস্থায় একটি গােলাকৃতি লেন্সের ফোকাস বের করা। এ সমাধানটি বিজ্ঞানীদের কাছে বেশী জটিলরূপে পরিচিত। তা সত্ত্বেও এটি কেমন আলােড়ন সৃষ্টি করেছিল ১৮৮১ সালের ‘American Jourrnal of Mathematics’-এ প্রকাশিত Prof. Marcus Bakar-র প্রবন্ধে তার সম্যক পরিচয় পাওয়া যায়।
আল হাইসাম ত্রিকোণমিতিতে বেশ উপাদেয় অবদান রেখেছেন। দিক নির্ণয় করবার বিষয়ে তার অন্যতম গ্রন্থ ‘মাকালাতু মুছর ফি সামলে কিবলা’ গ্রন্থে তিনি ত্রিকোণমিতির কোটেনজেন্ট সম্বন্ধে একটি থিওরেম উদ্ভাবন করেন। আল হাইসাম ক্যাটোপট্রিকন্দ্রে উপর গবেষণা করেছিলেন, যা আল হাজেনের সমস্যা বলে পরিচিতঃ
“Draw lines from two points in the plane of the circle which meet the circumference at a point and make equal angles with the normal at that point”.
এই সমস্যা আমাদের সমীকরণের চতুর্থ-মাত্রায় নিয়ােজিত করে। আল হাইসাম হাইপ্যারাবােলা ইন্টারসেক্টিং-এ সার্কেলের সাহায্যে তার সমাধান করেছিলেন। এইভাবে তিনি আল মাহানি-র (কিউবিক) সমীকরণেরও সমাধান করেছিলেন। তবে আল হাইসামের বিজোড়া খ্যাতি তার আলােক সংত্রান্ত গবেষণার উপর প্রতিষ্ঠিত। তার প্রায় প্রত্যেক রচনাতে বীজগণিত ও জ্যামিতির বহুল প্রয়ােগ দেখা যায়। তার গ্রন্থগুলি পড়লে মনে হবে, এটা যেন ১৭ শতকে রচিত কোনও বিখ্যাত ইউরােপীয় পদার্থবিজ্ঞানীর। বস্তুত গ্যালিলিওর গবেষণা ও রচনা পদ্ধতির সঙ্গে আল হাইসামের বৈজ্ঞানিক তৎপরতার ও রচনার সাদৃশ্য বিশেষ লক্ষণীয়।
বিশ্বকোষ প্রস্তুতকর্তা আবু রাইহান মহম্মদ ইবনে আহমদ আলবিরুনী (মৃঃ ১০৪৫), যার মধ্যে বহু অসাধারণ গুণের সমন্বয় লক্ষ করা যায়। তিনি ছিলেন গাণিতিক, জ্যোতির্বিদ, দার্শনিক, ভৌগলিক এবং ভ্রমণকারী। গণিতে তাঁর অসাধারণ। ব্যুৎপত্তির জন্য তাকে সর্বকালের সেরা বিজ্ঞানী হিসাবে অনেকে চিহ্নিত করেন। তিনি ভ্রমণ রসিক ছিলেন। তাই ভারতবর্ষে বহুদিন অতিবাহিত করেছিলেন এবং ভারতীয় প্রাচীন ভাষা সংস্কৃত থেকে বহু গ্রন্থ আরবী ভাষায় অনুবাদ করেছিলেন। এইভাবে মুসলমান জনগণের সঙ্গে ভারতীয় জনগণের একটা যােগসূত্রও তিনি স্থাপন করেছিলেন। তিনি বহু বৈজ্ঞানিক জ্ঞানের অবতারণা করেছিলেন। তাঁর আরবী সংখ্যার একটা সুস্পষ্ট ধারণা এবং কোণের ত্রিছেদ পদ্ধতির ব্যাখ্যা সর্বজনবিদিত। পরবর্তীকালে তিনি আরও বহু সমস্যার সমাধান করেছিলেন (যা আলবিরুনীর সমস্যা বলে পরিচিত), যা কোন Ruler বা শুধুমাত্র compass দ্বারা সাধিত হতে পারে না।

‘কানুনে মাসউদী’-তে ত্রিকোণমিতির অধ্যায়টি দেখলেই বুঝা যায় তিনি কত বড় বৈজ্ঞানিক সাধক করেছিলেন। তিনি প্রথমত ০° ডিগ্রী থেকে ৯০° sine- এর মূল্য নির্ধারণ করে একটি sine table তৈরী করেন। পূর্ববর্তী অন্যান্য তালিকা থেকে এর পার্থক্য হলাে যে এখানে আলবিরুনী শুধু প্রত্যেক ডিগ্রির sine নির্ধারণ করেই ক্ষান্ত হননি, প্রতি ডিগ্রির অংশেরও sine নির্ধারণ করেছেন। প্রত্যেক ১৫ মিনিট অংশ বৃদ্ধির জন্য sine-এর পরিমাণের যে তারতম্য হয়, তার মূল্য দশমিকের সপ্তম স্থান পর্যন্ত নির্ধারণ করে তিনি তাঁর কাজ সমাপ্ত করেন। কাজটি যে কি বিপুল অধ্যবসায় এবং পরিশ্রমসাপেক্ষ গাণিতিক মাত্রেই সে কথা উপলব্ধি করেন। এই তালিকা তৈরি করতে তিনি যে পদ্ধতি অবলম্বন করেন তাকে চার ভাগে ভাগ করা যেতে পারে। প্রথমে তিনি সুষম বহুভুজের বাহুগুলি ঠিক করে নিয়ে তা থেকে 60°, 309, 45° sine-এর পরিমাণ নির্ধারণ করেন। এরপরে ত্রিকোণমিতি এবং জ্যামিতি উভয়ভাবেই sin (A+B)-র ফর্মূলা নির্ণয় করে B=A ধরে নিয়ে তা থেকে sin 2A -এর পরিমাণ নির্ধারণ করার পন্থা বের করেন। তৃতীয় পন্থাটি গাণিতিক বৈশিষ্ট্যতার জন্য বিশেষভাবে উল্লেখযােগ্য। বিজ্ঞানের দিক থেকে এটি তখনকার দিনের তুলনায় অনেক উন্নত ভাবনার পরিচায়ক। বিজ্ঞানীকে যে এর জন্যে কি অপরিসীম পরিশ্রম এবং অধ্যবসায়ের পরিচয় দিতে হয়েছে সে বুঝতে পারা যাবে তার কার্যকলাপ থেকেই। কাজটি হলাে ১৫ ডিগ্রির sine নির্ধারণ করা। কিন্তু এর জন্যে দরকার হয় ত্রৈমাত্রিক সমীকরণের সমাধান। জ্যামিতিক ভাষায় একে বলা যেতে পারে চাপের একতৃতীয়াংশের জ্যা নির্ধারণ করা। স্তরে স্তরে গণনা করে এই ত্রৈমাত্রিক সমীকরণ সমাধান করার জন্যে আলবিরুনী তার গ্রন্থের কয়েকটি পরিচ্ছেদ ব্যবহার করতে বাধ্য হয়েছেন। চতুর্থ দফায় sin (A+B) ফর্মুলা বারবার প্রয়ােগ করে তালিকাটি সম্পূর্ণ করেন।
শুদ্ধ ও সুক্ষ্ম গণনায় আলবিরুনীর প্রবর্তিত নিয়ম এক বিস্ময়। মুসলিম বিজ্ঞানীদের অনেক বৈপ্লবিক কৃতিত্ব ইউরােপীয় চৌর্যবৃত্তির কবলে পড়ে তাদেরই আবিষ্কার বলে চালিয়ে দেওয়া হয়েছে। আলবিরুনীর প্রবর্তিত এই নিয়মটি তারমধ্যে অন্যতম। তাঁর এ আবিষ্কার বর্তমানে ‘The formula of Interpolation’ নামে নিউটনের উদ্ভাবন বলে চালানাে হচ্ছে। অথচ নিউটনের জন্মের বহু পূর্বে আলবিরুনী এ আবিষ্কারই করেননি শুধু, এর ব্যবহার করে বিশুদ্ধ sine তালিকা তৈরী করেন। তিনি তাঁর সাইন তালিকা এত সুক্ষ্মভাবে গণনা করেছেন যে এতে ভুলের পরিমাণ খুব কম। বলা প্রয়ােজন যে, বর্তমানেও এর চেয়ে সুক্ষ্মতর গণনা হয়নি এবং কোনও বৈজ্ঞানিক গণনাতেই আঙ্কিক বিশুদ্ধ গণনা নেওয়া হয় না। নির্দিষ্ট কোণের sine নির্ধারণ করার ফর্মুলা বের করেই আলবিরুনী ক্ষান্ত হননি। এর বিপরীত পন্থাটিও তিনি অতি সুনিপুণভাবে বের করেছেন। এর মধ্যে তার সুকৌশলী বৈজ্ঞানিক মনের পরিচয় পাওয়া যায়।
সমতলিক মণ্ডলাকার ত্রিভুজের সমাধানের জন্য তিনি ফর্মুলার উদ্ভাবনা ও বৈজ্ঞানিক উপায়ে সেগুলিকে প্রতিষ্ঠিত করার জন্যও যত্নবান হয়েছেন। বিজ্ঞানী অনেক পরিশ্রম সহকারে এগুলিকে বৈজ্ঞানিক ভিত্তিতে স্থাপন করে এদের ত্রিকোণমিতির মর্যাদা দিয়েছেন। তাঁর সমাধান বিজ্ঞানীদেরকে কিভাবে আকৃষ্ট করেছিল তার প্রমাণ পাওয়া যায় আড়াইশাে বছর পর মারাঘার শ্রেষ্ঠতম বিজ্ঞানী নাসিরউদ্দিন তুসির ঠিক এই একই পন্থা ব্যবহার করা থেকেই। ত্রিকোণমিতির নব জীবনদানকারী হিসাবেই নাসিরউদ্দিন বিজ্ঞানজগতে সুপরিচিত। ত্রিকোণমিতির নানা সমস্যার সমাধান তাঁকে বিজ্ঞানজগতে অমর করে রেখেছে। কিন্তু এতে তিনিও আলবিরুনীকেই অনুসরণ করেছেন মাত্র। আলবিরুনীর কার্যাবলীর সঙ্গে বিশেষ পরিচয় না থাকার জন্য তার অনেক কাজই অন্যের নামে প্রচলিত হয়ে পড়েছে। ত্রিকোণমিতির ফর্মুলার ব্যাপারেও এর ত্রুটি হয়নি। Prof. Braunmuhle তাঁর ‘Histroy of Trigonometry’-তে আলবিরুনীর কার্যের সঙ্গে অপরিচয়ের জন্যেই এই ফর্মুলাটিকে নাসিরউদ্দিনের আবিষ্কার বলে মত প্রকাশ করেছেন। মণ্ডলাকার সমকৌণিক ত্রিভুজের ৬টি কৌণিক সম্বন্ধের মধ্যে ৪টি গ্রীক বিজ্ঞানীদের দ্বারা আবিষ্কৃত হয়। আলবেরুনীর পূর্ব পর্যন্ত এর ওপর বিশেষ উন্নতি সাধিত হয়নি। তিনিই সর্বপ্রথম অন্য দুটি আবিষ্কার করেন এবং ত্রিকোণমিতিকে নতুন রূপ দিয়ে একে সর্বাঙ্গসুন্দর করে তােলেন। এই ফর্মুলা দু’টি হলঃ
Cos A = Cos a Sin B
Cos c = Cot A Cot B
বলা বাহুল্য, এই ফর্মুলা দু’টি প্রতিষ্ঠা করেই বিজ্ঞানী ক্ষান্ত হননি। নিজস্ব প্রমাণের সঙ্গে সঙ্গে মেনেলাউসের Theorem দিয়ে এই দু’টি প্রমাণ করেও এদের বৈজ্ঞানিক ভিত্তি সুপ্রতিষ্ঠিত করেন। তার প্রত্যেক কাজের মধ্যে এমনই একটি সত্যান্বেষী মনের সন্ধান পাওয়া যায়। পূর্ব থেকে প্রচলিত বলেই যে তাকে নির্বিচারে সত্য বলে মেনে নিতে হবে এ যে তার প্রকৃতি-বিরুদ্ধ। তিনি প্রত্যেকটি প্রচলিত বৈজ্ঞানিক মতবাদ নিজের জ্ঞানমতাে যাচাই করে নিয়ে তবে স্বীকার করেছেন। পূর্বেরগুলিকে যাচাই করে নিয়ে আবার তার নতুন প্রমাণ নিতেও কসুর করেননি। এমনই একটির উদাহরণ হল Sin A = Sin B ফর্মুলা Sin a Sin b
তিনি নিজেই বলেছেন, এটি সাবিত ইবনে কুরার উদ্ভাবিত। কিন্তু এর সত্যতা স্বীকার করা সত্ত্বেও নিজস্ব প্রমাণ দিতেও ত্রুটি করেননি তিনি। আলবিরুনীর বিরাট পান্ডিত্যের অনেকখানিই বহু শতাব্দী যাবত আধুনিক বিশ্বের নজরে কুয়াশা সৃষ্টি করেছিল। প্রফেসর সাখাও এবং Prof. Ramsay Wright-এর অনুবাদ প্রকাশের পর বিধের দৃষ্টি আকৃষ্ট হয়। বর্তমান দুনিয়ার সর্বত্রই তাঁর কার্যাবলীর আলােচনা হচ্ছে। ইউরােপে ‘International Congress of Orientalist’ ১৯৪৮ সালের জুলাই মাসে প্যারীতে ২১তম অধিবেশনে তাঁর জন্ম সহস্রবার্ষিকী পালন করে। এখানে প্রসঙ্গত বলে রাখা যেতে পারে যে, আলবিরুনী বহুভুজের বাহুসমূহের পরিমাণ বীজগাণিতিক সূত্রে লিপিবদ্ধ করেন। এ বিষয়ে তিনি আল খােয়ারিজমী প্রমুখ। পূর্বেকার বিজ্ঞানীদের পন্থা অনুসরণ করে সাধারণ সূত্র এবং ফল সবই কথায় প্রকাশ করেন।
এই প্রসঙ্গেই টলেমি এবং ইয়াকুবের প্রসঙ্গ এসে পড়ে। তারা দুজনেই ত্রৈমাত্রিক সমীকরণের সমাধানের কোনও চেষ্টা না করেই সমস্যাটির সমাধান করতে চেষ্টা করেন। আলবিরুনী উদাহরণ দিয়ে দু’জনের পদ্ধতিকেই অবৈজ্ঞানিক প্রমাণ করে তীব্র সমালােচনা করেছেন।
কোণকে সমত্রিখন্ডিত করার গাণিতিক সমস্যার এখন পর্যন্ত কোনও সমাধান হয়নি। পূর্বেকার বিজ্ঞানীদের এ সমস্যার সম্মুখীন হতে হয় নানা গাণিতিক বিষয়ের আলােচনা প্রসঙ্গে। সমাধানের চেষ্টাও অনেকেই করেন। আলবিরুনীকেও এ সমস্যার সম্মুখীন হতে হয়। গাণিতিক সমাধান অসম্ভব জেনেই তিনি চেষ্টা করে ১২টি যান্ত্রিক উপায় বের করেন। এই যান্ত্রিক উপায়ের মধ্যে তার অসামান্য প্রতিভার পরিচয় পাওয়া যায়। এইভাবেই তিনি ১৭ ডিগ্রি চাপের যে পরিমাণ নির্ধারণ করেন তা দশমিকের দশম স্থান পর্যন্ত শুদ্ধ।
এখন আমরা ওমর খৈয়ামের গাণিতিক কর্মপদ্ধতির উপর আলােকপাত করব, যিনি মধ্যযুগের একজন সুখ্যাত গাণিতিক এবং জ্যোতির্বিদ বলে পরিচিত। তিনি বিখ্যাত কবিও ছিলেন। একই ব্যক্তিতে এমন কবি প্রতিভার সঙ্গে এমন অসামান্য বৈজ্ঞানিক প্রতিভার সমন্বয়ের দৃষ্টান্ত ইতিহাসে বিরল। তার বীজগণিতের কর্মপদ্ধতি গ্রীক এবং আল খােয়ারিজমীর জ্ঞানকে এতটাই উন্নতির শিখরে নিয়ে গিয়েছিল যে, তা অন্যান্য মুসলমান বীজগাণিতিকদের ছাড়িয়ে গিয়েছিল। এই বিজ্ঞানের বিকাশ সাধনে তাঁর অবদান শ্রদ্ধার সঙ্গে স্মরণীয়।

খােয়ারিজমী যেখানে শুধুমাত্র চতুষ্পদ সমীকরণ (কোয়াড্রিনােমিয়াল) নিয়ে আলােচনা করেছিলেন, ইনি সেখানে কিউবিক সমীকরণের উপর অধিক তথ্য সরবরাহ করেছিলেন। তিনি সমীকরণের উল্লেখযােগ্য বিভাজন করেছিলেন, যা সমীকরণের জটিলতার উপর প্রতিষ্ঠিত ছিল। সপ্তদশ শতাব্দীর প্রারম্ভে সমীকরণের আধুনিক বিভাগ প্রতিষ্ঠিত হয়েছিল, বিশেষত সমীকরণের মাত্রার উপর ভিত্তি করে। তবে এখানে মনে রাখতে হবে যে, তিনি কিউবিক সমীকরণকে ২৭টি শ্রেণীতে বিভক্ত করেছিলেন, যা চারটি প্রধান অধ্যায়ে বিভক্ত ছিল। তিনি ঐ সমস্ত সমস্যার সমাধানের চেষ্টা করেছিলেন এবং একই সঙ্গে তাদের সীমাবদ্ধতারও উল্লেখ করেছিলেন। সমীকরণে ক’টি পদ থাকবে সেই হিসেবে শ্রেণী বিভাগ করা হত, যেমন ত্রিপদ, চতুষ্পদ সমীকরণ ইত্যাদি। চতুষ্পদ সমীকরণের কয়েকটি নমুনা হল –
x2 + bx2= cx + d
x3 + cX = bx2 + d
x3 + d = bx2 + cx
এই জাতীয় সমীকরণের সমাধান কল্পে ওমরের বিশেষত্ব এই যে, তিনি প্রধানত জ্যামিতির আশ্রয় গ্রহণ করেছেন। জ্যামিতির প্রয়ােগ দ্বারা নানা বীজগাণিতিক সমস্যার সমাধান প্রচেষ্টা অবশ্য সাধারণভাবে আরবীয় গণিতবিদদের বৈশিষ্ট্য। এই প্রচেষ্টায় ওমর আবার তাদের মধ্যে অগ্রগণ্য। এমন প্রচেষ্টা হতে এক প্রকার বিশ্লেষণমূলক জ্যামিতির উদ্ভব ঘটে। ১৬ ও ১৭ শতকের বিখ্যাত ফরাসী গণিতবিদ কোর্ট কর্তৃক উদ্ভাবিত বিশ্লেষণমূলক জ্যামিতি হতে এটা নানা বিষয়ে আলাদা হলেও, এমন জ্যামিতির প্রথম আলােচনা কৃতিত্ব অবশ্যই আরবীয় গাণিতিকদের প্রাপ্য। ইউক্লিডের স্বীকার্য সত্য এবং সামান্য গ্রীককরণের উপর তিনি অনুসন্ধান করেছিলেন। ১৮৫১ সালে ওমর খৈয়ামের বীজগণিত ফরাসী ভাষায় এফ ওয়েপেক-র দ্বারা প্যারিসে ‘লা অ্যালজেবরা ডি-ওমর আল খৈয়ামী’ নামে সম্পাদিত ও অনূদিত হয়েছিল। আল খােয়ারিজমী এবং ওমরের অন্তর্বর্তীকালে আরব্য বীজগণিতের যে কি পরিমাণ উৎকর্ষ সাধন ঘটেছিল, এই গ্রন্থ তার প্রমাণ। তারপর গণিতের এই বিভাগে গ্রীকদের তুলনায় আরবীয়রা যে কতদূর অগ্রসর হয়েছিল, ওমরের বীজগণিতের পর্যালােচনা করলে সে সম্বন্ধে আর কোনও সন্দেহ থাকে না।
বীজগণিত বিষয়ক তার গ্রন্থটি ১০টি অধ্যায়ে এবং মােটামুটি ৫টি বিষয় বিন্যাসে সমাপ্ত—
১. বীজগণিতের সংজ্ঞাসমূহের ব্যাখ্যাসহ ভূমিকা।
২. সরল ও যৌগিক সমীকরণসহ যে সকল সমীকরণ সমাধানের প্রস্তাব করা হয়েছে সেগুলাের তালিকা।
৩. প্রথম ও দ্বিতীয় মাত্রা সমীকরণের আঙ্কিক ও জ্যামিতিক সমাধান।
৪. ভগ্নাংশীয় সমীকরণ সম্পর্কে আলােচনা।
৫. বিজ্ঞানী আবুল জুদের কার্যাবলী আলােচনা। খৈয়ামের ‘আল জাবর ওয়াল মুকাবালা’ নামে এই গ্রন্থটির পাণ্ডুলিপি লিডেন ও প্যারিস লাইব্রেরীতে বর্তমান রয়েছে।
বীজগণিতের একটি বিশেষ শাখা হল ‘Binomial theorem’ ওমর খৈয়াম সর্বপ্রথম এ নিয়ে সুস্পষ্ট পথ নির্দেশ করেন। বর্তমানে ‘Binomial theorem’-এর আবিষ্কর্তা হিসাবে বিজ্ঞানী নিউটনের নাম উচ্চারিত হয়, কিন্তু প্রধান আবিষ্কারক ছিলেন ওমর খৈয়াম। ‘মুসকিলাতে হিসাব’ হল তার অপর গণিত বিষয়ক গ্রন্থ।
যাইহােক, ত্রিঘাত সমীকরণের সমাধানের জন্য কণিক রেখার অবতারণা করতে হয়। পূর্বোক্ত চতুষ্পদ সমীকরণগুলির ক্ষেত্রে সাধারণত দুটি পরাবৃত্তের সাহায্য নিতে হয়। পরাবৃত্ত দুটির প্রকৃত স্বরূপ কেমন হবে এবং তারা পরস্পরকে ছেদ করবে কিনা এটা নির্ভর করে x এর গুণক b-র মানের উপর।
কণিক জ্যামিতির সাহায্যে ত্রিঘাত সমীকরণ সমাধানের চেষ্টা গ্রীক গণিতবিদ মেনেক মাসের মধ্যেও কিছুটা লক্ষ করা গিয়েছিল। তিনি x3-2a3 = 0 এই সমীকরণে x -এর মূল নির্ধারণ করেছিলেন। অবশ্য তার উদ্দেশ্য ছিল অন্য। একটি ঘনর দ্বিগুণ আয়তনের আর একটি ঘন কিভাবে রচনা করা যায়, এটাই ছিল তার সমাধানের আসল উদ্দেশ্য। সাধারণভাবে বীজগণিতের কোনও ত্রিঘাত সমীকরণের সমাধান নির্ণয় সম্ভব নয়। তবে কণিক জ্যামিতির সাহায্যে ওমর যেভাবে কঠিন ত্রিঘাত সমীকরণের সমাধান করতেন তাতে এই জ্যামিতির উপর তার যে অগাধ দখল ছিল, বিশেষ করে অ্যাপােলােনিয়াস প্রমুখ গ্রীক গণিতবিদদের উদ্ভাবিত কণিক জ্যামিতিতে তিনি যে বিশেষ দক্ষ ছিলেন, এটা নিঃসন্দেহ। কোর্ট তার ‘জিওমেট্রি’ গ্রন্থে ত্রিঘাত সমীকরণ সমাধানের উদ্দেশ্যে ওমর খৈয়ামের পদ্ধতি অবিকল অনুসরণ করেছেন।
বর্তমানে প্রচলিত গ্রেগরীয়ান বর্ষপঞ্জি সর্বত্র গ্রহণযােগ্য রূপ পেয়েছে। কিন্তু এর চেয়ে আধুনিক ও নিখুঁত ক্যালেন্ডার প্রণয়ন করেছেন ওমর খৈয়াম। হিট্টিরও সপ্রশংস ভাষা-
“The researches of Umar al-khayyam and his Collaborators resulted in the production of the calendar named after his patron at-Tarikh al Jalali, which is even more accurate than the Gregorian Calendar. The Later leads to an error of one day in 3330 years, whereas al-Khayyam’s apparently lead to an error of one day in 5000 years”.
ওমরের সমকালে দ্বাদশ শতাব্দীর গণিত আলােচকদের মধ্যে রয়েছেন ফাজারী (-১১২২), মনসুর আল খাজিনি, হাকিম লুকরী, মােহাম্মদ কাজীন, নাজিব ওস্তি, মামুর বায়হাকী, ইবনে কুশাক, আবদুল বাকী, খারাকী (-১১৩৮), আবদুল মালেক সিরাজী, ইবনুদ দাহহান (-১১৯১), আদনান আল আইনজাবরী (-১১৫৩)
স্পেনের আবুস সালাত (১০৬৭) গণিতে ‘রিসালা ফিল আম বিল আস্তারলব’ গ্রন্থ রচনা করেন। এতে তিনি আস্তারলব ছাড়াও Mechanics এবং Hydrostatics নিয়েও আলােকপাত করেন। জাবির বিন আফলাহ (১১৪০ খ্রীঃ) ত্রিকোণমিতি ও জ্যোতির্বিজ্ঞানে নতুন মতবাদ প্রতিষ্ঠিত করে টলেমীর মতবাদকে প্রচন্ড ঝাকুনি দেন। তিনি টলেমী উদ্ভাবিত ‘rule of six quantities’-র বৈজ্ঞানিক শুদ্ধতার ত্রুটি ঘােষণা করেন এবং একে বৈজ্ঞানিক অগ্রগতির অন্তরায় হিসাবে চিহ্নিত করেন। এর পরিবর্তে তিনি ‘rule of four quantities’ প্রচলন করেন। এ থেকেই তিনি গােলীয় সমকোণী ত্রিভূজের ত্রিকোণমিতিক সূত্রসমূহ আবিষ্কার করেন, যা তাকে গণিতে অমর করে রেখেছে। বিন আফলাহ জ্যোতির্বিজ্ঞানের উপর একটি গ্রন্থ রচনা করেছিলেন, যার আরবী নাম ছিল ‘কিতাব-আল-হাইআহ’ অথবা ইসলাহ আল-মাজিস্তি’। এতে তিনি ত্রিকোণমিতির উপর এক গুরুত্বপূর্ণ ভূমিকা লিখেছিলেন।
দ্বাদশ শতাব্দী থেকেই বিজ্ঞানে মুসলিম প্রাধান্য কমতে থাকে, তবুও কোনও কোনও মুসলিম বিজ্ঞানী মাঝে মাঝে ফুলকির মতাে জ্বলে উঠেছেন। ত্রয়ােদশ শতাব্দীতে ইবনে ইউনুস (১২৪২ খ্রীঃ) ‘Theory of numbers’ আলােচনায় বিশেষ কৃতিত্বের পরিচয় দেন। তাঁর এ অবদানই শ্রেষ্ঠতম অংকবিদ হিসাবে তাকে প্রতিষ্ঠিত করেছে। তিনি বীজগণিত, স্কোয়ার নাম্বার, রেগুলার হেপ্টাগণ ও আরও অনুরূপ বিষয়ের উপর পুস্তিকা রচনা করেছিলেন। তিনি সম্রাট দ্বিতীয় ফ্রেডারিকের জটিল প্রশ্নের সমাধান করেছিলেন। প্রশ্নটি ছিল- “How to construct a square equivalent to a circular segment?” সমস্যাটি যথার্থভাবে প্রমাণ করেছিলেন ইবনে ইউনুসেরই এক ছাত্র, আল-মুফাজ্জল ইবনে উমর আল-আবহারী, যিনি এর উপর একটা প্রবন্ধও রচনা করেছিলেন। শরফউদ্দীন তুসি (মৃ.১২১৩), ইবনুল লুবিদি (জন্ম-১২১০, মৃ. ১২৬৭) গণিত বিষয়ক একাধিক গ্রন্থ লিখেছেন।
আল জারকালী (ল্যাটিন আরজাচেল) একজন সুবিখ্যাত জ্যোতির্বিদ ছিলেন, যিনি ত্রিকোণমিতির ছকের গঠনের উপর বিশেষ তথ্য পরিবেশন করেছিলেন। ইবনে আল-ইয়াসমিনি বীজগণিতের উপর একটি ছােট কবিতা রচনা করেছিলেন এবং মহম্মদ আল হাক্সার, যিনি দ্বাদশ কিংবা ত্রয়ােদশ শতাব্দীতে প্রসিদ্ধি লাভ করেছিলেন বিশেষত পাটীগণিত ও বীজগণিতের উপর তিনি পুস্তিকা রচনা করেন, যা ১২৭১ সালে হিব্রু ভাষায় অনুদিত হয়েছিল।
আল মালিক আল-শিরাজী যিনি অ্যাপােলােনিয়াসের ‘Treatise’-এর উপর সংক্ষিপ্তসার তৈরি করেছিলেন, এবং আররাজি, যিনি একজন সুবিখ্যাত পণ্ডিত এবং দার্শনিক ছিলেন, তিনি ইউক্লিডের স্বীকার্য সত্যের উপর বহু তথ্য পরিবেশন করেছিলেন। মহম্মদ ইবনে আল- হাসার যিনি ইবনে ইউনুস এর সহায়তায় ‘রিসালাহ আল-বিরকার-আল-তামাম’ নামে পুস্তিকা রচনা করেছিলেন। Perfect compass ছিল এক প্রকারের যন্ত্র যার সাহায্যে সকল প্রকার কনিক টানা যেত।
গাণিতিক ইবনে বদর, যিনি বীজগণিতের (‘ইখতিসার-আল-জবর ওয়াল মুকাবালাহ’) সংক্ষিপ্তসার রচনা করেছিলেন। গ্রন্থটিতে গাণিতিক এবং সংখ্যাগত তথ্য ও উদাহরণে পূর্ণ ছিল। এতে Quadratic equations, Surds, Multiplication of palynomials, Arithmetical theory of proporttion, linear Diaphantine equations এবং অনুরূপ বিভিন্ন সমস্যার উল্লেখ ছিল।
মরক্কোর খ্যাতনামা জ্যোতির্বিদ, গাণিতিক এবং ভৌগােলিক আল হাসান আল মারাকাশী, যিনি সম্ভবত ১২৬২সালে প্রসিদ্ধি লাভ করেছিলেন। তিনি বিশেষত জ্যোতির্বিজ্ঞানের উপর বহু গ্রন্থ আমাদের উপহার দিয়ে গিয়েছেন। তাঁর প্রধান কাজ হিসাবে গৃহীত হয়েছিল ‘জামি আল মাবাদী ওয়াল গায়াত’। এটাকে জ্যোতির্বিজ্ঞানের ব্যবহারিক ও পদ্ধতিগত জ্ঞানের যথার্থ পুস্তক বলে অনেকে চিহ্নিত করেছিলেন। এতে ত্রিকোণমিতি এবং নমােনিক জ্ঞান সম্বন্ধেও আলােচনা ছিল। তিনি এতে শুধুমাত্র sine এবং versed sine-র উল্লেখ করেননি বরং পরিপূরক sine ও গঠন করেছিলেন যাকে ‘জাইব তামাম’ বলা হত।
মরক্কোর অপর সুখ্যাত গণিতবিদ ও ত্রয়ােদশ শতাব্দীতে যিনি অধিক জনপ্রিয়তা অর্জন করেছিলেন—তার নাম আবুল আব্বাস আহমদ ইবনে মহম্মদ। তিনি প্রায় ৭৪টি গ্রন্থের রচয়িতা ছিলেন, যার অধিকাংশই ছিল গণিত ও জ্যোতির্বিজ্ঞানের উপর। তার সুবিখ্যাত গ্রন্থের নাম ছিল ‘আল-তালখিস্ আন-আল-হিসাব’, যা প্রায় দুই শতাব্দী যাবৎ পঠিত হয়েছিল। পরবর্তীকালে এই গ্রন্থের উপর বহু কমেন্টারীও রচিত হয়েছিল। কমেন্টেটরদের মধ্যে ইবনে খালদুনের নাম বিশেষ উল্লেখযােগ্য। ১৮৬৪ খ্রিস্টাব্দে গ্রন্থটির ফরাসী অনুবাদ প্রকাশিত হয়। এটা একটা গাণিতিক সংক্ষিপ্তসার হিসেবে পরিচিত ছিল, যার মধ্যে গণিতের বহু সুখকর বৈশিষ্ট্যসহ ভগ্নাংশের বিকাশশীল পদ্ধতি, হিন্দি সংখ্যার প্রভূত প্রয়ােগ ইত্যাদি ছিল। তাছাড়াও এখানে Summation of squares and cubes, Casting out of nines, eights 47 sevens, rule of double false position ইত্যাদির উল্লেখ ছিল।
তালখিস্ ছাড়াও লেখক হিসাবশাস্ত্রের উপর আরও চারটি পুস্তিকা রচনা করেছিলেন, যা পূর্ণসংখ্যা, ভগ্নাংশ, অনুপাতের উপর লিখিত ছিল। তিনি Binomials এবং Apitomes-এর উপর পুস্তিকাও তৈরি করেছিলেন। তিনি ইউক্লিডের উপর একটা ভূমিকা এবং ভূমির পরিমাণ সম্পর্কে একটা পুস্তিকা প্রস্তুত করেছিলেন।
এখন আমরা নাসিরউদ্দিন তুসির গাণিতিক কর্মের উপর আলােকপাত করব, যার মধ্যে প্রভূত গুণের সমাবেশ ছিল। তিনি একজন খ্যাতনামা দার্শনিক, গাণিতিক, জ্যোতির্বিদ, চিকিৎসক এবং বৈজ্ঞানিক ছিলেন। আরবী ও ফারসি ভাষায় তার অসাধারণ বুৎপত্তি এবং গণিত ও বিজ্ঞানে তার অসাধারণ দক্ষতার জন্য তাকে তৎকালীন সেরা বিজ্ঞানী ও গাণিতিক হিসেবে গণ্য করা হত। তিনি ১২০১ খ্রিষ্টাব্দে খােরাসানের তুস শহরে জন্মগ্রহণ করেন। ১২৫৮ খ্রিস্টাব্দে আব্বাসী খিলাফত শেষের পর তিনি হালাকু খানের মন্ত্রিত্ব লাভ করেন। তিনি মােট ৬৪ খানি মূল্যবান গ্রন্থ আমাদের উপহার দিয়েছেন। জ্যামিতি ও বীজগণিতের উপর তিনি বহু গ্রন্থ রচনা করেছেন এবং পাটিগণিতের জ্ঞানও তার অজানা ছিল না। তার ‘সাকল আল কাত্তা’ মধ্যযুগের সর্বশ্রেষ্ঠ ত্রিকোণমিতির গ্রন্থ হিসেবে পরিচিত। ১৮৯১ সালে কনস্টান্টিনােপল হতে কারাথিয়ােডরি পাশা এর একটি ফারসি অনুবাদ (ট্রেইট ডু কোয়াড্রিলেটার) প্রকাশ করেন। প্রাঞ্জল ভাষায় শৃঙ্খলার সঙ্গে গ্রন্থটি রচিত হয়। মেনেলাউস ও টলেমির পদ্ধতি প্রথম প্রথম অনুসৃত হলেও তার উদ্ভাবিত বহু মৌলিক পদ্ধতির বর্ণনা এই গ্রন্থে রয়েছে। তিনি জ্যামিতির অন্তনিহিত মূল সমস্যা সহ প্রমাণ করেন যে, দুটি বিজোড় চতুর্ভুজ কখনাে চতুর্ভুজ হতে পারে না। তিনি আরও প্রমাণ করেন যে, যদি কোন বৃত্ত আভ্যন্তরিকভাবে অপর কোন দ্বিগুণ ডায়ামিটার সম্বলিত বৃত্তকে ছেদন করে এবং দুটি বৃত্তই যদি একইভাবে বিপরীত দিকে পাক খায় তবে পরিশিষ্ট স্পর্শক এবং ছােট বৃত্তটির গতি বড়টির চেয়ে দ্বিগুণ হবে, এবং তখন ছােট বৃত্তটির প্রকৃত সংযােগ কেন্দ্রটি বড় বৃত্তটির ডায়ামিটারের সঙ্গে গতিশীল হবে। জ্যামিতিতে তাঁর যে উদ্ভাবন তা ইউক্লিডের পূজ্য মতবাদকে দূরে ঠেলে দিয়ে নতুন যুগের সূচনা করে। তার একটি মতবাদ বর্তমানে ‘Non Euolidan Geometry’ নামে পরিচিত। অষ্টাদশ শতকের গণিতজ্ঞ সাকেরী এই মতবাদ উদ্ভাবনের কর্তা হিসাবে পরিচিত হলেও নাসিরউদ্দিনই এর প্রথম আবিষ্কারক।

‘Spherical Trigonometry’ এর সঙ্গে ‘Plane Trigonometry’-এর দিকেও তিনি আকৃষ্ট হন। সাইন সম্বন্ধ যে ‘Plane Trigonometry’-তেও খাটে তা তিনিই প্রথম তুলে ধরেন। ‘Spherical Trigonometry’-র সূত্র ষষ্ঠক তিনি স্পষ্টভাবে প্রয়ােগ করেন, টলেমীর জবরজঙ্গ প্রথা থেকে অংকবিদরা রেহাই পান। টলেমীর স্থানে বর্তমানে নাসিরউদ্দিনের সরল পন্থাগুলােই অনুসৃত হয়। তার পরিপূরক সংখ্যা নিয়মটি সাধারণভাবে কোণ ও বাহুর সম্বন্ধ দেখিয়ে দেয়-
Sin A = Sin B = Sin C
Sin a Sin b Sin c.
অর্থাৎ কোণগুলির সাইন বাহুগুলির সাইনের অনুপাত, এটা তিনি প্রমাণ করেন। এই প্রসঙ্গে-
Sin b = tan c সূত্রটিও নাসিরুদ্দিনের আবিষ্কার। তিনি ত্রিকোণমিতিকে যে স্তরে উন্নীত করেন, বহুদিন পর্যন্ত তা অতিক্রম করা সম্ভব হয়নি।
তিনি পিথাগােরাসের উপপাদ্যের প্রমাণ দিয়ে মারাঘায় গ্রহণ, সমীকরণ প্রভৃতি বিষয়ে গবেষণা পরিচালনা করেছিলেন। তিনি সেই যুগের যাবতীয় বৈজ্ঞানিক জ্ঞানের আকর ষােলটি গণিত গ্রন্থের সম্পাদনা করেন।
নাসিরউদ্দিনের ‘সাকল-আল কাত্তা’-গ্রন্থের পর গাণিতিক এবং জ্যোতির্বিদ আল মাঘরিবী একই নামে পুস্তক রচনা করেন। এই পরবর্তী গ্রন্থটি পূর্ববর্তীটির সঙ্গে খুব আংশিক সম্বন্ধযুক্ত ছিল, এবং এটা পুরাতন তত্ত্বের বিশেষ বিকাশ বলে গণ্য করা যেতে পারে। উদাহরণস্বরূপ, এটা সাইন তত্ত্বের দুটি প্রমাণসহ সমকোণী আনুভূমিক ত্রিভুজের সম্পর্ক নির্ণয় করে, যার মধ্যে একটা প্রমাণ নাসিরউদ্দিন থেকে পৃথক ছিল। তাছাড়া লেখক ইউক্লিডের উপাদানসমূহ, অ্যাপােলােনিয়াসের কনিকস (ক্ষুদ্র ভূমিকাসহ), ওডােসিওসের গােলক ও অন্যান্য সমস্যার উপর বহু তথ্য আমাদের উপহার দিয়েছেন, যা আজও শ্রদ্ধার সঙ্গে স্মরণীয় হয়ে আছে।
পতন যুগে আরও অনেক গণিত প্রতিভা জন্ম লাভ করেন। পারস্যের নৃপতি বিখ্যাত জ্যোতির্বিদ উলুগ বেগ, তার সহকারী জামসিদ বিন মাসুদ আল ফাসরী (১৪৩৬ খ্রীঃ), স্পেনের সর্বশেষ শ্রেষ্ঠ গাণিতিক আলী বিন মুহাম্মদ আল কালাসাদী (১৫৮৬ খ্রীঃ), কনস্টান্টিনােপালের মুহাম্মদ বিন মারুফ, বাহাউদ্দীন আমিলী গণিতে মৌলিক প্রতিভার স্বাক্ষর রেখেছেন।
এই রচনায় প্রধানত মৌলিক গণিতবিদদের নাম ও সংক্ষেেপ কার্যাবলী তুলে ধরা হয়েছে। প্রথম যুগ থেকে অন্তর্বর্তী সময়ে আরও বহু বিজ্ঞানী ও গণিত প্রতিভার নাম উল্লেখ করা যেতে পারে। গণিতের শাখা জ্যোতির্বিজ্ঞানে শত শত মুসলিম মনীষীর জীবন ও কার্যাবলী যুক্ত হয়েছে। তাদের সব পরিচয় এখানে দেওয়া হয়নি বিষয়ভুক্তির কারণে। মুসলিম গবেষকদের দানে জ্যোতির্বিজ্ঞান নিজেই আলাদা ফর্মে দাঁড়িয়ে গেছে। প্রধান মুসলিম বিজ্ঞানীদের প্রায় সবাই কম বেশী এ নিয়ে গবেষণা করেছেন এবং নিজেদের উদ্ভাবনী ক্ষমতার নজির স্থাপন করেছেন সগৌরবে। স্পেনে মুসলমানদের পতনপরবর্তী ধ্বংসযজ্ঞ বিশেষ করে মুসলিম জ্ঞানবত্তার পরিচয়বাহী লক্ষ লক্ষ পুস্তক পুড়িয়ে নদীতে ডুবিয়ে ধ্বংস করা না হলে, মােঙ্গলদের হাতে বাগদাদের লাইব্রেরীগুলির একই অবস্থা না হলে হয়তাে মুসলিম জ্ঞান-বিজ্ঞানের ইতিহাস অন্যভাবে লেখা হত। মূল জ্ঞানভান্ডার ধ্বংস সাধনের পর ও বিক্ষিপ্তভাবে প্রাপ্ত গবেষণার পরিণতিতে মুসলমানদের যে বিশাল অবদান আজ পরিলক্ষিত হয় তা বহুগুণ বর্ধিত হত তা বলা নিষ্প্রয়ােজন। যেটুকু জানা যাচ্ছে তাতে আজ কট্টর প্রাচ্যবিদরাও মুসলিম সভ্যতাকে প্রাপ্য সম্মান দিতে কসুর করছেন না, অথচ এক সময় তারা মুসলিম যুগকে অন্ধকার যুগ বলে নাক সিটকিয়ে নিজেদের হীনমন্যতাকে বার বার বাড়িয়ে তুলত। আজ ইউরােপ স্বীকার করতে বাধ্য যে, আধুনিক পাশ্চাত্য সভ্যতায় প্রকৃত নির্মাতা আরবরাই।
গণিত শাস্ত্রের অন্যান্য আলােচকদের মধ্যে আরও রয়েছেন-সনদ ইবনে আলী (-৮৬৪) আল হাজ্জাজ, আল্ জুরজানী, অনুবাদক হােনায়েন ইবনে ইসহাক (৮১০-৮৭৩), ইসহাক বিন হােনায়েন (৯১০ খৃ.), আল আরজানি (৮৫২), আল হিমসি (৮৮৩), আল ফজল (৮১৫), আহমদ ইবনে ইউসুফ (৯১২), আল্ ফারাবী, আল নাইরেজী (৯২৩), আল খাসিব, ইবনুল আদামী, ইবনুল আমাজুর (জন্ম, ৮৫৫), আবু ওসমান, আবু যাইদ, আবুল ফতেহ, আবদুর রহমান সুফী (৯০৩-৯৮৬), আবুল কাসেম (৯৮৫), আল সাগানী, আল কোয়াবিসী, আবুল ফজল জাফর, শরফউদ্দৌলা (৯৮৯), আল হামদানী, আবু আবদুল্লাহ, আবুল ফারাজ, আল মাজরিতি, আবু নাসের, আন নাসাভী, ইবনে সীনা, ইবনুস সামাহ (১০৩৫), ইবনে সাইদ (১০২৯-১০৭০), ইবনুল কারনিব, সিনান বিল আল ফতেহ প্রমুখসহ আরও অনেকে।
আগেই বলা হয়েছে, মুসলিম বিজ্ঞানীদের গবেষণার স্বীকৃতি আগের যে কোনও সময়ের চেয়ে সমকালে বেশী হচ্ছে, যদিও অসংখ্য আবিষ্কার এখনও অন্য নামে চলছে যথারীতি। ১৯৭১ সালে ‘International congress of Astronomers’-এ ‘International Astronomical Union’ কর্তৃক চন্দ্রপৃষ্ঠের তিনটি আগ্নেয়গিরির মুখের নাম রাখা হয়েছে। তিনজন বিশিষ্ট মুসলিম বিজ্ঞানীর নামে। তাঁরা হলেনঃ আলবিরুনী, ইবনে সীনা ও ওমর খৈয়াম। এরও পূর্বে ১৯৩৫ সালে চাদের ১৩টি ‘Lunar formation’ ১৩ জন মুসলিম বিজ্ঞানীর নামে নামকরণ করা হয়েছিল, তারা হলেনঃ আবদুর রহমান। সুফী, উলুগ বেগ, মাশাআল্লাহ, ফারগানী, বাত্তানী, সাবিত বিন কুরা, ইবনুল হাইসাম, আল যারকালী, জাবির বিন আফলাহ, নাসিরউদ্দিন, আল বিতরুজী, আবু আল ফিদা ও খলীফা মামুন।
১ থেকে ৯ এবং শূন্য (সি) সংখ্যাগুলির ইতিহাসেরও একটি স্পষ্ট ও বৈজ্ঞানিক আলােচনা প্রয়ােজন যাতে সেগুলির প্রামাণিক উৎপত্তি ও গুরুত্ব প্রকাশিত হয়। মাত্র দশটি সংখ্যার যাদুতে এবং সেগুলিতে শূন্য আরােপ করে কোন ব্যক্তি অন্তহীন সংখ্যার সেট, যেমন দশ, একশ, লক্ষ লক্ষ এমনকি কোটি কোটি সাজাতে পারে। মানুষ যখন দশটি সংখ্যা উদ্ভাবন করল এবং সেগুলি মিলিয়ে সেগুলিতে মূল্য আরােপ করল তখন গাণিতিক চিন্তার ক্ষেত্র ত্বরিৎ ঘটে গেল।
প্রখ্যাত গ্রীক চিন্তানায়ক অ্যারিস্টটল এই গাণিতিক সংখ্যাগুলির কল্যাণ ছাড়াই জীবন যাপন করেছেন। এমন কি পিথাগােরাসের এই গভীর গাণিতিক কৌশল সম্পর্কে কোন ধারণাই ছিল না। আলেকজান্দ্রীয়রা এ রকম সূক্ষ্ম বিষয়ের কোন চিন্তাই করতে পারেনি। নবম শতকে শ্রেষ্ঠ মুসলিম বৈজ্ঞানিক প্রতিভার পক্ষে এক উল্লেখযােগ্য বাঞ্ছিত লাফ দেওয়া সম্ভব হল। সমগ্র পাশ্চাত্য জগতের কাছে ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯ সংখ্যাগুলি যে আরবীয় সাংখ্যমানের প্রতীক ছিল এবং বিশ শতকের শেষের দিকে তা যে বিজ্ঞানের গৌরবের চরম শিখরে পৌঁছেছে তা কে অস্বীকার করতে পারে। শূন্য সংখ্যাটি (সিফর) যার নিজের প্রকৃত কোন মূল্য নেই, কিন্তু গণিত শাস্ত্রে যার প্রভূত মূল্য আছে তা আল-খােয়ারিজমী কর্তৃক উদ্ভাবিত হয়েছিল। অক্ষর থেকে শূন্যসহ সকল সংখ্যাপ্রতীককে পছন্দ করে তিনি সংখ্যা ব্যবহারের প্রথম নায়কের মর্যাদা লাভ করেছিলেন।
এটি স্বতঃসিদ্ধ সত্য যে, ন’টি আরবীয় সংখ্যা এবং শূন্য ব্যবহার করে ও সেগুলিতে শূন্য আরােপ করে অন্তহীন সংখ্যার সেট তৈরি করে বিজ্ঞানের ক্ষেত্রে মুসলিম পণ্ডিত ও বৈজ্ঞানিকগণ পৃথিবীকে এক খাঁটি মূল্যের উপহার দিয়েছেন। তাদের বাদ দিলে, পরবর্তীকালে যা দৃষ্টি গােচর হয়েছে সেই স্পুটনিকও আসত না, পরিগণকও (কমপিউটার) আসত না। তাদের বাদ দিলে। পদার্থবিজ্ঞানের ক্ষেত্রে যে কোন ধরনের বৈজ্ঞানিক অগ্রগতি ত্বরান্বিত হওয়া ব্যাহত হত।
পাশ্চাত্য দেশে ও সমগ্র পৃথিবীতে সংখ্যাসমূহ ব্যবহার ও প্রচলনের ক্ষেত্রে এবং সেগুলিতে মূল্য আরােপ করে বিরাট সম্ভাবনায় ফলপ্রসূ করার বিষয়ে আরবীয় বৈজ্ঞানিকগণ যে প্রথম ছিলেন তাতে কোন সন্দেহ নেই। এইচ জি ওয়েলস্ তার ‘আউট লাইন অব হিস্ট্রি’ গ্রন্থে মন্তব্য করে বলেছেন যে, আল খােয়ারিজমী নামের একজন মুসলিম গণিতবিদ সংখ্যাসমূহের উপর মূল্য আরােপ করেছিলেন। প্রখ্যাত পণ্ডিত জর্জ সারটোন মনে করেন যে, মুহাম্মদ বিন ইবরাহিম আল ফাজারি কর্তৃক ভারতীয় গ্রন্থ ‘সিদ্ধান্ত’-র অনুবাদই সম্ভবত ইসলামে ভারতীয় সংখ্যাসমূহের প্রচলন হওয়ার কারণ। কিন্তু একথা অস্বীকার করা যাবে না যে, তখনও পর্যন্ত ঐ সংখ্যাগুলি কেবল প্রতীক ছিল এবং সেগুলি প্রায় অব্যবহৃত ও সুপ্ত ছিল। নিঃসন্দেহে, জ্ঞানবিজ্ঞানের সকল ক্ষেত্রে বিভিন্ন সাংখ্যমানের ব্যবহারিক রূপ দেওয়ার ক্ষেত্রে মুসলমানরা নেতৃত্ব গ্রহণ করেছিল এবং সমগ্র পৃথিবীতে তারাই দশমিক পদ্ধতি চালু করেছিল ।
সংখ্যার মূল্যের উপর ভিত্তি করে আরবীয় সাংখ্যমান পদ্ধতি যা আমরা আজকের দিনে কোন সংখ্যা—একক অঙ্ক থেকে কোটি কোটি সংখ্যা, তা লেখার উৎস হিসাবে দেখছি, এ বিষয়ে কোন বিতর্কের প্রয়ােজন নেই সেটি ছিল নবম শতকের মুসলমান বৈজ্ঞানিকদের এক অনন্য অবদান। এর পূর্বে এমন কি মুসলমানরাও শব্দের প্রতীক ব্যবহার করে সংখ্যা বুঝাত।
সবচেয়ে আশ্চর্য বিষয় হল যে, সেদিনের ইউরােপ প্রায় চার শতক ধরে এটির প্রচলন প্রতিহত করে রােমান সংখ্যা পদ্ধতির উপর ভিত্তি করে ও জটিল রােমান গণনা-পদ্ধতি আঁকড়ে ছিল। যে কেউ এটা অনুমান করবে যে বৈজ্ঞানিক ও সাংস্কৃতিক বিষয় এ রকম কুসংস্কারাচ্ছন্ন ও সঙ্কীর্ণমনা দৃষ্টিভঙ্গি কেবল সেই অবদান যােগাতে পারে যাকে ইউরােপের অন্ধকার যুগ বলে অভিহিত করা হয়েছে।
মুসা আল খােয়ারিজমীর পাণ্ডিত্যপূর্ণ গ্রন্থসমূহ প্রধান উৎস ছিল, যার মধ্য দিয়ে আরবী সংখ্যাসমূহ পাশ্চাত্যে পরিচিত হয়ে উঠেছিল। সেটি ছিল নবম শতক ও তার পরের বিষয়। কিন্তু সভ্যতার অগ্রগতির চারশ বছর পিছনে থেকে কেবল তের শতকে ইউরােপ এটির সর্বাপেক্ষা মূল্যবান শক্তি (কার্যকারিতা) অনুধাবন করল। ইউরােপের এই ক্ষতি গুরুতর ছিল। সে যুগে মুসলমানদের কাছে অপ্রধান বেহালা বাজানাের অবস্থানেও তারা ছিল না। সমগ্র যুগ ধরে ইউরােপ অন্ধকারে, আলাের পিছনেই ছিল।
মুসলিম বৈজ্ঞানিকদের উদ্ভাবন শক্তির সর্বাপেক্ষা শ্রেষ্ঠ নিদর্শন হল শূন্যের আবিষ্কার। শূন্য কোন কিছুর প্রতীক না হয়েও অন্যান্য নয়টি অঙ্কের মূল্যের অবস্থানে বসে মূল্য পরিগ্রহণ করল।
আরবীয়দের কাছে ‘শূন্য’ ছিল ‘সিফর’ যার অর্থ হল শূন্যগর্ভ। শূন্য উৎপত্তির পূর্বে, সংখ্যাগুলি দাবা খেলার জন্যে ছক কাটা বাের্ডের উপর লেখা হত এবং একটি বর্গাকার ক্ষেত্রকে পরিত্যক্ত রাখা হত এটি বুঝাবার জন্যে যে, পরিস্থিতি এখন শূন্য গর্ভ। পাটিগণিতের অঙ্ক কষার জটিল পদ্ধতি শূন্য আগমনের সঙ্গে সঙ্গে অত্যন্ত সরল ও সহজ হয়ে গেল। একের পাশে তিনটি শূন্য বসিয়ে দাও, তখন সংখ্যাটি হাজারে দাঁড়িয়ে যাবে। একের পাশে পাঁচটি শূন্য বসালে এটি লক্ষ পর্যবসিত হবে এবং এভাবে মূল্যবৃদ্ধি ঘটবে।
এ বিষয়ে যে কেউ বিস্মিত হবে যে, দ্বাদশ শতকের শেষ পর্বের আগে পর্যন্ত শূন্যকে ব্যবহার করার প্রজ্ঞা ও দূরদৃষ্টি ইউরােপের ছিল না, সম্ভবত পুরাতন রােমান সংখ্যাসমূহ পরিত্যাগ করার সাহস তাদের ছিল না। যে কোন সংখ্যাকে কেবল দশটি প্রতীকের সাহায্যে প্রকাশ করার গুরুত্বপূর্ণ ধারণাটি তাদের কাছে অত্যন্ত বৈপ্লবিক ছিল।
সেদিনের বিস্তৃত মুসলিম সাম্রাজ্যে সংখ্যাসমূহের ব্যবহারের বিষয় বেশ কিছু লােক নাও জানতে পারেন। মুসলিম পাশ্চাত্য দেশ (স্পেন ও উত্তর আফ্রিকা) শূন্যের প্রতীক হিসাবে বৃত্ত ‘০’ কে এবং তথাকথিত আরবীয় সংখ্যাগুলিকে ব্যবহারের জন্য গ্রহণ করে। মুসলিম প্রাচ্য (বাগদাদ ও সংলগ্ন ভূখণ্ডসমূহ) শূন্যের প্রতীক হিসাবে বিন্দুকে গ্রহণ করে ও সংখ্যাসমূহের বিবর্তন ঘটায়। ১ ২ ৩ ৪ ৫ ৬ ৭ ৮ ৯—এই স্কীমটি আজও উর্দু ও ফারসিতে বিদ্যমান আছে। ইউরােপ আরবীয় সংখ্যাসমূহের অনুসরণ করেছে।
আল খােয়ারিজমীর পাণ্ডিত্যপূর্ণ গবেষণা গ্রন্থ ‘আল হিসাব আল-জবর ওয়াল মুকাবলা’ আট শতাধিক উদাহরণ দিয়ে উপস্থাপিত করা হয়েছে। ‘অ্যালজেবরা’ নামটির মধ্যে তার গ্রন্থ অংশত টিকে আছে এবং এটির ব্যবহারিক চরিত্র নিঃসন্দেহে এটির টিকে থাকার পিছনে অবদান যুগিয়েছে।
এই গ্রন্থ দিয়ে ইউরােপে বীজগণিত শাস্ত্র অধ্যয়ন প্রচলিত হল এবং এর সঙ্গে আল খােয়ারিজমীর নামও প্রচলিত হল, কারণ গ্রন্থটি দ্বাদশ শতকে ল্যাটিন ভাষায় অনূদিত হয়েছিল এবং যােড়শ শতকের পূর্ব পর্যন্ত ইউরােপের বিশ্ববিদ্যালয়সমূহে গণিতের প্রধান পাঠ্যপুস্তক হিসাবে ব্যবহৃত হয়েছিল।
উপরােক্ত গ্রন্থখানির প্রভাব ইউরােপে এত অধিক হয়েছিল যে গ্রন্থখানির নাম সমীকরণ তত্ত্বের সঙ্গে সমার্থক হয়ে উঠেছিল। পাশ্চাত্য ভূখণ্ডে আরবীয় সংখ্যাসমূহ প্রচলনের বিষয়ে আল খােয়ারিজমীর গ্রন্থের অবদান আছে, এই রীতিকে পরবর্তীকালে ‘আলগরিদম’ বলা হত।
এই বিখ্যাত বৈজ্ঞানিকের আর একটি গ্রন্থ ছিল দশমিক প্রণালীর উপর, যা ল্যাটিন ভাষায় অনূদিত হয়ে সংরথিত হয়েছে। নিঃসন্দেহে, তিনিই দশমিক চিহ্ন প্রচলনের ক্ষেত্রে প্রথম ছিলেন এবং অঙ্কসমূহের উপর অবস্থানের মূল্য আরােপ করেছিলেন। তিনি পূর্ণরূপে অবগত ছিলেন যে সঙ্গীতের সুর ও ছন্দ, সেগুলির যথার্থতা গণিত শাস্ত্রের উপর নির্ভর করে, তাই তিনি তার গাণিতিক নিবন্ধের সঙ্গে সঙ্গীতশাস্ত্রের একটি অংশ সংযােজন করেছিলেন।
ব্যারন কাররা দ্য ভক্স ‘লিগ্যাসি অব ইসলাম’ গ্রন্থে সংখ্যাসমূহের উৎপত্তির বিষয়ে সুন্দরভাবে বর্ণনা করেছেন। আল খােয়ারিজমীর ‘দ্য নুমেরাে ইন্ডিকো’ গ্রন্থটি সংখ্যাসমূহের উৎপত্তি বিষয়ে প্রায়-আলােচিত প্রণটি উত্থাপন করেছে। প্রাচ্যদেশে প্রচলিত বর্ণমালার অক্ষর দিয়ে গণনা করার বিপরীতে সংখ্যা দিয়ে গণনা করার রীতি যাকে আমরা আরবীয় রীতি বলে থাকি তাকে আরবীয় পণ্ডিতরা ভারতীয় (হিন্দু) হিসাব পদ্ধতি বলে অভিহিত করেন। কিন্তু আমরা দ্রুত সিদ্ধান্ত যেন অবশ্যই না নিয়ে ফেলি যে, সেগুলির প্রকৃত উৎপত্তি ভারতবর্ষে ছিল। আরবী ভাষায় প্রকৃতপক্ষে ‘হিন্দি’ শব্দটি ‘হিন্দাসি’ শব্দের সঙ্গে গুলিয়ে ফেলা হয়। ‘হিন্দাসি’ শব্দটির তাৎপর্য হল জ্যামিতি কিংবা ইঞ্জিনিয়ারের কলা-কৌশল সংক্রান্ত বিষয়, এবং যেখানে ‘হিন্দি’ শব্দ ব্যবহৃত হয় সেখানে নানা ক্ষেত্রে ‘হিন্দাসির’ অর্থ প্রয়ােগ আরও উত্তমরূপে খাপ খায়। এভাবে জ্যোতির্বিজ্ঞানে মাত্রাবিভক্ত বৃত্ত আছে যাকে ‘হিন্দি’ বলে অভিহিত করা হত। কিন্তু সম্ভম্বত তাকে ‘গাণিতিক বৃত্ত’ বলে অর্থ করা উচিত। তাই এভাবে (হিন্দি) অভিহিত সংখ্যাগুলিকে সহজভাবে গাণিতিক বৈশিষ্ট্য সম্পন্ন প্রতীক বলে ভাবা যেতে পারে। অন্যদিকে পারসিকরা সংখ্যাসমূহকে ‘প্রান্ত-সংখ্যা’ বলত, তাদের ভাষায় যার অর্থ হল ‘ছােট বা বুদ্র পরিমাণের বৈশিষ্ট্য সম্পন্ন। সংখ্যাসমূহের আকার প্রসঙ্গে ওপেক সংস্কৃত ভাষায় সংখ্যাগুলির নামের আদ্যাক্ষর থেকে সেগুলির উদ্ভব হয়েছে বলে মনােভাব পােষণ করতেন। সংখ্যাসমূহের রূপের সম্বন্ধ মােটেই স্পষ্ট যে নয় সে তথ্য বাদ দিলেও পাটিগাণিতিক পদ্ধতিসমূহের মধ্যে যেখানে অক্ষরসমূহ ব্যবহৃত হয়। সেখানে সংখ্যাসমূহের আদ্যাক্ষর ব্যবহার হওয়াটাই রীতি নয়, সেখানে বর্ণমালার অক্ষর ক্রমানুসারে ব্যবহৃত হয়। এই রীতি গ্রীকদের মধ্যে ছিল, আরবীয়দের নিজেদের মধ্যে ছিল। আলবিরুনী মন্তব্য করেছেন যে, ভারতীয় নকশার সবচেয়ে সুন্দর রূপ থেকে সংখ্যাসমূহ উদ্ভূত হয়েছে। তবে তিনি সঠিক বলেননি এই রূপটা কি, কিংবা ভারতের কোন অংশে তার ব্যবহার ছিল। অপরপক্ষে এটি প্রতীয়মান হয় যে, পৃথিবীর অপর যে কোন অংশ থেকে আরবীয়দের মধ্যে সংখ্যাসমূহের একটি সহজতর ও কুশলীতর রূপ উদ্ভূত হয়েছিল এবং এটিই ছিল অবশ্যই তাদের মূলরূপ। প্রথম পাঁচটি অঙ্ক ১, ২, ৩, ৪, ৫ যুক্তাক্ষরের আঁচড়ে গঠিত হয়েছে, পরের চারটি অঙ্ক সম্ভবত সহজ প্রচলিত প্রথায় গঠিত হয়েছে। শূন্য হল একটি ক্ষুদ্রাকার বৃত্ত কিংবা বিন্দু। সম্ভবত আরবীয়রা এই চিহ্নগুলি নয়া- প্লেটো মতাদর্শের ঐতিহ্য থেকে লাভ করেছিল।
আমরা জানি যে, সাংখ্যমান পদ্ধতির মধ্যে শূন্য সংখ্যাটি এক প্রধান গুরুত্ব বহন করে, কারণ এই শূন্যই সংখ্যাসমূহের দশ, দশের কোনও গুণিতক, শত ইত্যাদি শক্তিতে সাংখ্যমানটি নিয়ে যেতে আমাদের সক্ষম করে। শূন্য সংখ্যাটি যদি না থাকত তাহলে আমাদের একক, দশক, শতক ইত্যাদির স্তম্ভ দিয়ে সারণী ব্যবহার করে প্রতিটি সংখ্যাকে তার স্থানে রাখতে হত। এই সারণীকে বলা হয় অ্যাবাকাস। আমরা দেখতে পাই যে, পাশ্চাত্যের জনগণের কাছে শূন্য পরিচিত হওয়ার অন্তত ২৫০ বছর পূর্বে আরবীয়রা শূন্য সম্পর্কে জ্ঞান রাখত। রােমে বুয়েথিয়াসের নিকট পঞ্চম শতকে প্রথম অ্যাবাকাস রীতি দেখা যায়, কিন্তু তখন এর ব্যবহার বিস্তৃত হয়নি। দশম শতকে জারবার্টের দ্বারা এই নীতির পুনরাবির্ভাব হয়। জারবার্ট স্পেনে ভ্রমণ করেছিলেন এবং মূরদের বিজ্ঞানসমূহ অধ্যয়ন করেছিলেন। তিনি অ্যাবাকাসের ব্যবহারকে প্রসারিত করেছিলেন, কিন্তু শূন্যের সঙ্গে তার পরিচিতি হয়নি। দ্বাদশ শতকে খ্রিস্টান পাটিগণিতবিদগণ স্তম্ভ ছাড়াই এবং শূন্য দিয়ে পরিপূরণ করে গণনারীতির উপর নিবন্ধাদি লিখতে শুরু করেন। এই রীতিটিকে ‘আলগরিদম’ বলে অভিহিত করা হয়েছিল। আরবীয়দের মধ্যে প্রথম থেকেই শূন্য নিয়েই সংখ্যাসমূহ প্রকাশিত হয়।
এটি লক্ষণীয় যে, ল্যাটিন ‘সি’ শব্দটির দুটি অর্থ আছে। এটি মাঝে মাঝে শূন্য বুঝাতে ব্যবহৃত হয়, আবার মাঝে মাঝে তুচ্ছ ব্যক্তি বা বস্তু বুঝায় শূন্য অর্থে, এটি স্পষ্টত আরবীয় ‘সিফর’ অর্থাৎ শূন্যগর্ভ বুঝায়, আবার সংখ্যাবাচক কিছু বুঝালে এটি লিখিত কোন কিছু যেমন, একটি বই বা চরিত্র বুঝায়। ‘অ্যালজেবরা’ ‘সাইফার’, ‘লগারিদম’ প্রভৃতি শব্দসমূহ গণনা, বিজ্ঞানের প্রতিষ্ঠা ও পরিব্যাপ্তিতে আরবীয়রা যে ভূমিকা পালন করেছিল তার সাক্ষ বহন করে।
তবে ১২০২ খ্রিস্টাব্দে পিসার অধিবাসী লিওনার্ডো ফাইবােনাক্কি তার একটি বইতে প্রথম আরবীয় (হুরূফ আল গুবার) সংখ্যার ব্যবহার শুরু করেন। পি কে হিট্টি বলেন,
“সত্যকথা বলতে কি লিওনার্ডো ফাইবােনাক্কির বইয়ের মধ্য দিয়েই ইউরােপে গণিত শাস্ত্রের প্রচলন হয়েছিল। পুরনাে ধরনের সংখ্যার সাহায্যে পাটিগণিতের অগ্রগতি অসম্ভব হয়ে পড়ত। আজ যে ধরনের গণনা প্রক্রিয়ার সঙ্গে আমরা পরিচিত, তার মূলে রয়েছে শূন্য এবং আরবী সংখ্যাগুলাের উপস্থিতি।”
একথা থেকে বুঝা যায় যে, বর্তমানে আমরা যে শূন্য ব্যবহার করছি তা ভারতীয় শূন্য নয়, এটি আরবদের আবিষ্কৃত ‘হুরূফ আল গুবার’-এর অনুকরণে। হিট্টি এই ‘হুরূফ আল গুবার’ (আরবীয় সংখ্যাতত্ত্ব) প্রচলনকে মাইল ফলক বলেছেন। তাই আল খােয়ারিজমী থেকে বর্তমান ইউরােপ শব্দগুলি (অ্যালজেবরা, আলগরিদম, সাইফার) অকুণ্ঠায় গ্রহণ করেছেন। উত্তরকালে গণিত শাস্ত্রের উন্নতি ও গণিতের সাহায্যে বিজ্ঞানের অন্যান্য শাখায় যে সব আবিষ্কার আজ পর্যন্ত অব্যাহত ধারায় হয়ে আসছে, তার বেসিক টুল বা মৌলিক যন্ত্র হিসেবে এই গণনা নীতিগুলির যে ব্যাখ্যা ও ব্যবহার আল খােয়ারিজমী করেছেন, তার অসামান্য মূল্য আজ বৈজ্ঞানিক মাত্রেই অকুণ্ঠ চিত্তে স্বীকার করেন। এইচ জি ওয়েলস তার ‘দ্য আউট লাইন অফ হিস্ট্রি’ গ্রন্থে বলেন,
“আল খােয়ারিজমীই শূন্যের আবিষ্কারক। যদিও ভারতীয়রাই শূন্যের আবিষ্কার করে এই মর্মে অনেকে দাবী করেন, কিন্তু এর সার্থক ও সফল প্রয়ােগের জন্যই আল খােয়ারিজমী শূন্যের আবিষ্কারক বলে নন্দিত হয়ে আছেন।”
পর্যালােচনার শেষে বিজ্ঞানী প্রফুল্লচন্দ্র রায়ের বক্তব্য উল্লেখ করা যেতে পারে,
“এ সময় প্রাচীন বিজ্ঞানের বিপুল প্রসারের পাশাপাশি নতুন নতুন বিষয় সংযােজিত হচ্ছিল। ভারতীয় পাটিগাণিতিক গঠন পদ্ধতি প্রবর্তিত হয়, এ এক তাৎপর্যপূর্ণ পদ্ধতির আবিষ্কার। এই পদ্ধতির মাধ্যমে সমস্ত সংখ্যাকেই এক থেকে দশ—এই কটি সংখ্যা দিয়ে প্রকাশ সম্ভব, এর ফলে গণনার ক্ষেত্র সরলীকৃত হলাে ও সমস্ত গাণিতিক গণনার ক্ষেত্রে নতুন দিগন্ত উন্মােচিত হলাে। বীজগণিত তথা বির্বজনীন পাটিগণিতে— অসংজ্ঞাত রাশির গণনা। সমস্ত ধরনের রাশির মধ্যে অন্তরসম্পর্ক অনুসন্ধান বা পাটিগাণিতিক বা জ্যামিতিক যাই হােক না কেন—সম্ভব হলাে। ডায়ােফ্যান্টাস যে বীজ রেখে গিয়েছিলেন তা থেকেই এগুলি পল্লবিত হয়েছিল। মহম্মদ বেন মুসা দ্বিঘাত সমীকরণের সমাধান তত্ত্ব ও ওমর বেন ইব্রাহিম ত্রিঘাত সমীকরণের তত্ত্ব আবিষ্কার করলেন। সারাসেনীয় পণ্ডিতেরা ত্রিকোণমিতিতেও আধুনিক রূপান্তর এনেছিলেন। আগে যেমন ছিল তার পরিবর্তে বৃত্তের জ্যাকে লম্ব ও অতিভূজের অনুপাত বা সাইনে প্রকাশ করে ত্রিকোণমিতিকে বিজ্ঞানের এক পৃথক শাখায় উন্নীত করেছিলেন। পূর্ববর্ণিত মুসা ছিলেন গােলকীয় ত্রিকোণমিতি প্রক্রিয়ার প্রণেতা জমি জরিপ সংক্রান্ত এমন অসাধারণ কাজ করেছিলেন যে সেগুলিকে এ বিষয়ের উপর গ্রীক পণ্ডিত ইউক্লিডের হারিয়ে যাওয়া কাজের অনুকৃতি বলে প্রচার করা হয়েছিল।”
সহায়ক গ্রন্থ ও প্রবন্ধ
- জর্জ সার্টন, ইন্ট্রোডাকশান টু দ্যা হিস্ট্রি অফ সায়েন্স, কার্নেগী ইনস্টিটিউট অফ ওয়াসিংটন, ১৯৫৩।
- জন উইলিয়াম ড্রেপার, এ হিস্ট্রি অফ ইনটেলেকচুয়্যাল ডেভেলপমেন্ট অফ ইউরােপ, লন্ডন, ১৯১০।
- আচার্য প্রফুল্লচন্দ্র রায়, ভারতবর্ষ ও ইসলাম (অভিভাষণ, আলিগড় মুসলিম বিৰ্থবিদ্যালয়, ১৯২৩) দেখুন-মুসলিম সমাজ এবং এই সময়, ২য় খন্ড, সম্পাদনা- মইনুল হাসান, ন্যাশানাল বুক এজেন্সি, ২০০৩।
- স্যার টমাস আরনল্ড ও আলফ্রেড গিলম, দ্যা লিগ্যাসি অফ ইসলাম, অক্সফোর্ড, ১৯৭৪- অনুবাদ-নুরুল ইসলাম পাটোয়ারী, ইসলামিক ফাউন্ডেশন বাংলাদেশ, ২০০০।
- কারা ডি ভক্স , অ্যাস্ট্রোনমি অ্যান্ড ম্যাথমেটিক্স (প্রবন্ধ)- দেখুন-স্যার টমাস আরনল্ড ও আলফ্রেড গিলম, দ্যা লিগ্যাসি অফ ইসলাম, অক্সফোর্ড, ১৯৭৪- অনুবাদ-নুল ইসলাম পাটোয়ারী, ইসলামিক ফাউন্ডেশন বাংলাদেশ, ২০০০।
- রবার্ট ব্রিফল্ট, দ্যা মেকিং অফ হিউম্যানিটি, ইসলামিক বুক ফাউন্ডেশান লাহাের, ১৯৮০।
- এম আকবর আলি, বিজ্ঞানে মুসলমানের অবদান, কলকাতা, ১৯৪৩।
- আব্দুর রহমান খান, মুসলিম কন্ট্রিবিউশান টু সায়েন্স অ্যান্ড কালচার, লাহাের, ১৯৪৬।
- সৈয়দ আমীর আলি, দ্যা স্পিরিট অফ ইসলাম- অনুবাদ-এম দরবেশ আলি খান, ইসলামিক ফাউন্ডেশন বাংলাদেশ, ১৯৯৩।
- পি কে হিট্টি, হিস্ট্রি অফ আরবস, লন্ডন, ১৯৭২- অনুবাদ-মল্লিক ব্রাদার্স, কলকাতা,১৯৯৬।
- কে আলি, মুসলিম সংস্কৃতির ইতিহাস, ঢাকা, ১৯৮১।
- ডঃ এম আব্দুল কাদের, মুসলিম কীর্তি, ইসলামিক ফাউন্ডেশন বাংলাদেশ, ১৯৮৮।
- ডঃ মরিস বুকাইল, দ্যা বাইবেল দ্যা কোরাণ অ্যান্ড সায়েন্স, ইউ এস এ, ১৯৭৮।
- আর এম সাভরি, ইনট্রোডাকশান টু ইসলামিক সিভিলাইজেশন, কেমব্রিজ ইউনিভার্সিটি প্রেস, ১৯৭৭।
- সমরেন্দ্র নাথ সেন, বিজ্ঞানের ইতিহাস, শৈবা প্রকাশন, কলকাতা, ১৯৯৪।
- জিয়াউদ্দিন সরদার, সায়েন্স টেকনােলজি অ্যান্ড ডেভেলপমেন্ট ইন দ্যা মুসলিম ওয়ার্ল্ড, লন্ডন, ১৯৭৭।
- এস লেনপুল, দ্যা মুরস ইন স্পেন, ১৯৫৯।।
- নুরুল হােসেন খন্দকার, বিশ্ব সভ্যতায় মুসলিম অবদান, ইসলামিক ফাউন্ডেশন বাংলাদেশ, ১৯৮৮।
- প্রফেসার জিয়াউদ্দিন আহমেদ, বিশ্বসভ্যতায় ইসলামের প্রভাব, লেখা প্রকাশনী, কলকাতা, ২০০৩।
- ডঃ মহম্মদ সাউদ, ইসলাম ও বিজ্ঞানের বিবর্তন, মল্লিক ব্রাদার্স, কলকাতা, ১৯৯৬।
- মুহাম্মদ নুরুল আমিন, বিজ্ঞানে মুসলমানদের অবদান, আহসান পাবলিকেশন, ঢাকা, ২০০২।
- চৌধুরী আতিকুর রহমান, মুসলিম বৈজ্ঞানিকদের ইতিহাস, তালিম প্রকাশনী, কলকাতা, ২০০৮।
- এম আকবর আলি, আলবিরুণী, ইসলামিক ফাউন্ডেশন বাংলাদেশ, ১৯৮২।
- শরিফুল ইসলাম সরকার, মুসলিম স্পেন, ইসলামিক ফাউন্ডেশন বাংলাদেশ, ১৯৮৭।
- ডঃ শামসুজ্জামান আহমেদ, ইসলাম ও জ্ঞান-বিজ্ঞান চর্চা (প্রবন্ধ)- দেখুন-মইনুল হাসান, পূর্বোক্ত, ন্যাশানাল বুক এজেন্সি, কলকাতা।
- ডব্লু ডব্লু রাউজ বল, এ শর্ট অ্যাকাউন্টস অফ দ্যা হিস্ট্রি অফ ম্যাথমেটিক্স, লন্ডন, ১৯০১।
- এইচ এ সালমন, রাইজ অ্যান্ড ফল অফ দ্যা আরব ডােমিনিয়ন।
- এইচ জি ওয়েলস, দ্যা আউট লাইন অফ হিস্ট্রি ।।
- জন বসাট, এ জেনারেল হিস্ট্রি অফ ম্যাথমেটিক্স ।
‘নবজাগরণ’ অ্যান্ড্রোয়েড অ্যাপ্লিকেশনটি প্লে স্টোর থেকে ডাউনলোড করতে নিচের আইকনে ক্লিক করুন।
‘নবজাগরণ’ এর টেলিগ্রাম চ্যানেলে জয়েন হতে নিচের আইকনে ক্লিক করুন।
‘নবজাগরণ’ এর ফেসবুক পেজে লাইক করতে নিচের আইকনে ক্লিক করুন।

 নবজাগরণ (ষাণ্মাসিক) – জীবনানন্দ ১২৫ তম জন্ম সংখ্যা – মননশীল সাহিত্য পত্রিকা
নবজাগরণ (ষাণ্মাসিক) – জীবনানন্দ ১২৫ তম জন্ম সংখ্যা – মননশীল সাহিত্য পত্রিকা